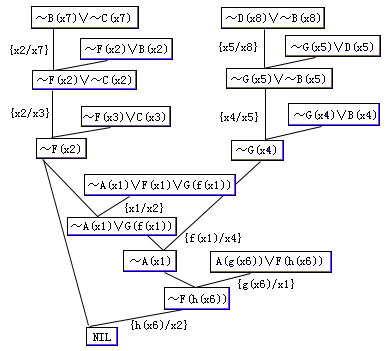
图4.12 例2的反演树

这个否定式可化为两个子句~B（x）∨~C（x）和~D（y）∨~B（y）。
这样，得到该问题的子句集如下（经过变量换名后）：

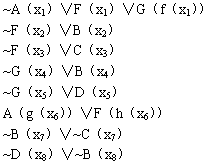
用归结反演法对基本集S进行演绎，可得反演树如图4.12所示。
为了要得到修改证明树，须根据以下两个子句来构造重言式：
~B（x7）∨~C（x7）∨（B（x7）∧C（x7））
~D（x8）∨~B（x8）∨D（x8）∧B（x8））
这两个重言式中出现了合取符号，不是子句表示的形式，因此在演绎修改证明树时，要把（B（x7）∧C（x7））和D（x8）∧B（x8））当作单文字式的整体来处理（因其中的元素不会取作为合一集的文字），这样便得到如图4.13所示的修改证明树，根部子句的公式是
（ x6）{[B（g（x6））∧C（g（x6））]∨[D（f（g（x6）））∧B（f（g（x6）））]∨[B（h（x6））∧C（h（x6））]}
可以看出这个回答语句的形式与目标公式略有不同，前两个析取元则与目标公式形式相同，第三个析取元[B（h（x6））∧C（h（x6））]也与目标公式的一个析取元相象。因此对于目标公式是析取范式时，提取回答过程将产生一个类似于目标公式部分的析取项，因而也可以把根部的语句作为问题的回答。

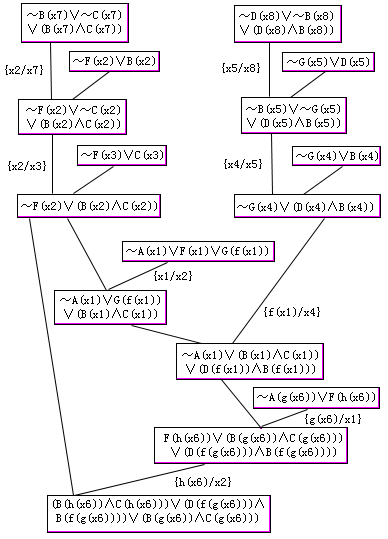
图4.13 例2的修改证明树