以下内容"2．提取回答的一般过程"不作为课内要求，作为扩展内容自学。

　　2．提取回答的一般过程
　　这一节将通过几个例子，说明提取回答过程应考虑的若干具体问题，最后给出回答提取的过程。
　　（1）回答中出现Skolem函数的情况
例1：已知：For all x and y，if x is the parent of y and y is the parent of z， then x is the grandparent of z. Everyone has a parent.
询问：Do there exist individuals x and y such that x is the grandparent of y?
表示成公式集后有
事实：（x）（y）（P（x，y）∧P（y，z））→G（x，z））
（y）（x）P（x，y）
目标公式：（x）（y）G（x，y）
用归结反演法很容易就给出目标公式的证明，其反演树如图4.10所示。图中母体子句中有横线标记的文字是归结时被合一的文字，子句P（f（w），w）中的Skolem函数f（w）可解释为w父亲的名字。图4.11是这个问题的修改证明树，根部的子句G（f（f（v）），v）是回答语句，形式与目标公式一致，其含义由公式（v）G（f（f（v）），v）表达，对于每一个v，及v的祖父，均是满足回答条件的那些个体的实例。

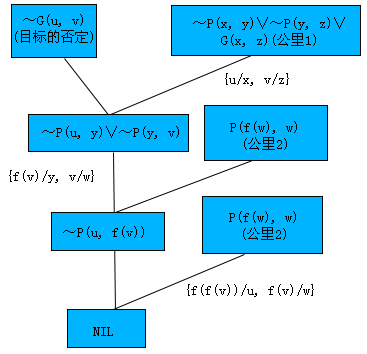
图4.10 例1的反演树

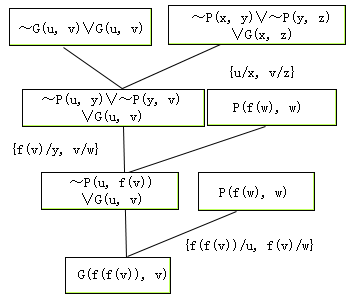
图4.11 例1的修改证明树

　　（2）目标公式是析取范式的情况
　　这种情况比较复杂，要规定一种方法来处理重言式中出现的合取符号，才能提取出答案来。
例2：设前提子句集是：
~A（x）∨F（x）∨G（f（x））
~F（x）∨B（x）
~F（x）∨C（x）
~G（x）∨B（x）
~G（x）∨D（x）
A（g（x））∨F（h（x））
目标公式：（ x）（ y）（（B（x）∧C（x））∨（D（y）∧B（y）））
先来看一下目标否定式的形式：
~（ x）（ y）（（B（x）∧C（x））∨（D（y）∧B（y）））
＝（ x）（ y）~（（B（x）∧C（x））∨（D（y）∧B（y）））
＝（ x）（ y）（（~B（x）∨~C（x））∧（~D（y）∨
~B（y）））