4.4 基于归结法的问答系统

　　归结反演系统主要用来解决证明的问题，即给定公式集F0，要求证明具有存在量词量化的目标公式（ x）W（x）。但有时我们希望能回答问题，即知道x的某一个取值或x的一个例，这就是问答系统的功能。对于直接回答x＝A时W（A）是否为真这种问题，可直接用归结反演系统证明，即可给出结果。而对x＝？时W（x）为真或填空类型的问题，则应是先证明一个与回答问题语句中提问项有对应匹配关系的一般语句，然后再找某一个具体的匹配值，该值就给出问题的回答。这种要求产生满足条件的x的例需要构造性的证明方法，即如果能给出对问题的构造性证明过程，那么就可能给出具体问题的回答。本节将通过具体例子讨论应用归结反演过程来提取问题的回答。

　　1．提取回答的方法
　　该例子根据已知条件"John在什么地方Fido就在什么地方"和"John在学校"，问"Fido在什么地方？"首先用归结法证明Fido确实在一个地方，然后再回答出Fido在什么地方。这是一个简单的例子，稍微复杂一点的例子，请参见4.6节的猴子摘香蕉问题。
例：If Fido goes wherever John goes and if John is at school， where is Fido?
这个问题给出两个已知事实和一个询问，这个询问的答案应从事实出发演绎得到。先把问题用谓词逻辑公式表示：
前提公式集：（x）（AT（John，x）→AT（Fido，x））
AT（John，School）
目标公式：（x）AT（Fido，x）
我们先要证明目标公式是前提公式集的逻辑推论，然后再找出一个x的例子，这样就回答了Fido在何处的询问。这里主要的关键是把询问表达为一个有存在量词约束的目标公式，这样就很容易用归结法给出证明，图4.8给出了该例的反演树。接着就是如何从反演树那里对所询问的问题提取一个回答，一个简单的办法其步骤是：

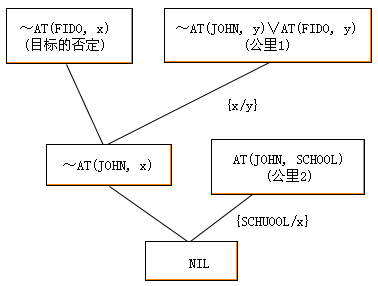
图4.8 例题的反演树

（1）用一个重言式来取代目标公式的否定式这个子句，该重言式为
~AT（Fido，x）∨AT（Fido，x）
（2）按反演树的构造进行归结，给出重言式替代目标否定式子句后的证明树，这时根子句不为空，称这个证明树为修改证明树，如图4.9所示。
（3）用根部的子句作为回答语句。
从图4.9看出根部有子句AT（Fido，School）就是一个正确的回答，这个回答与目标公式形式相同，它是目标公式中约束变量x用常量School替代的结果，即求得目标公式中x的一个例。

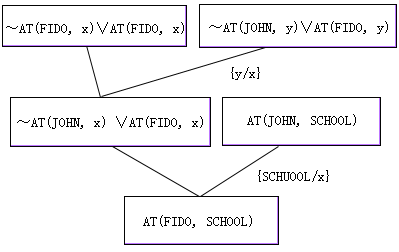
图4.9 修改证明树

　　从这个例子看出，回答的提取过程是把一棵归结反演树转化为根部带有回答语句的一棵修改证明树的过程。从证明树可以得出根部的语句是公理集（前提公式集）与一个重言式（由目标否定式构成）的逻辑推论，也就是扩大公理集的逻辑推论，因而修改证明树构造的本身就证明这种提取回答的办法是正确的。