（2）谓词逻辑的归结过程

　　对于谓词逻辑来说，可以这样判断两个子句是否可进行归结，及其归结式是什么。
　　对于子句C1'∨L1和C2'∨L2，如果L1与～L2可合一，且s是其合一者，则(C1'∨C2')s是其归结式。其中L1、L2是单文字。事实上L1、L2中有一个含有否定符，所以对另一个加上否定符后，才能判断它们是否可合一。

设C1和C2为两个不同的子句，子句中的变量已标准化。我们采用文字集的形式来表示子句（即文字之间理解为析取关系），则有
C1＝{C1i}（i＝1，2，…，n），C2＝{C2j}（j＝1，2，…，m）
再设{L1k}和{L2k}分别为C1和C2的两个子集。
若{L1k}和{~L2k}的并集存在一个mgu s，则两个子句的归结式为
C＝{{C1i}－{L1k}}s∪{{C2j}－{L2k}}s
可以看出对这两个子句进行归结时，由于有多种方式选取{L1k}和{L2k}，因此归结式不是唯一的。
例：C1＝P（x，f（A））∨P（x，f（y））∨Q（y）
C2＝~P（z，f（A））∨~Q（z）
①取L11＝P（x，f（A）），L21＝~P（z，f（A））存在s＝{z/x}使L11和~L21合一，所以归结式为
P（z，f（y））∨Q（y）∨~Q（z）
②取L11＝P（x，f（y）），L21＝~P（z，f（A））
则s＝（z/x，A/y），归结式为
Q（A）∨~Q（z）
③取L11＝Q（y），L21＝~Q（z）
则s＝{y/z}，归结式为
P（x，f（A））∨P（x，f（y））∨~P（y，f（A））
这个例子说明，选择不同文字对做归结时可得到不同的归结式，但由于都是用最一般的合一者作置换，因此这些归结式仍是最一般的归结式。就是说，如果对某个文字不是用mgu来合一，那么得到的归结式比最一般的归结式则有较多的限制。实际上我们总是希望用最一般的归结式，以增加归结过程的灵活性。
下面举一个简例说明谓词逻辑的归结过程。
例：已知：①会朗读的人是识字的；
②海豚都不识字；
③有些海豚是很机灵的。
证明：有些很机灵的东西不会朗读。

如果你不熟悉如何用谓词逻辑表达这些知识，请参阅有关数理逻辑或离散数学的书籍。
首先把问题用谓词逻辑描述如下：
已知：
①（x）（R（x）→L（x））
②（x）（D（x）→~L（x））
③（x）（D（x）∧I（x））
求证：（x）（I（x）∧~R（x））
再把前提条件的谓词公式进行化简，将要证明的结论取反并化成子句形，求得子句集：
由已知条件（1）得到。
（1）~R（x）∨L（x）
由已知条件（2）得到。
（2）~D（y）∨~L（y）
由已知条件（3）得到（两个子句）。
（3a）D（A）
（3b）I（A）
由结论的否定得到。
（4）~I（z）∨R（z）
从子句集求归结式，并将它加进子句集，连续进行直到产生空子句为止。下面的归结式序列代表一个可行的证明过程：
用归结树（归结反演树）的形式可以更清楚的表示归结的过程。本例的归结树如下图所示。其中有下划线的部分表示两个子句中的L1和L2，旁边标出的是它们的合一者。

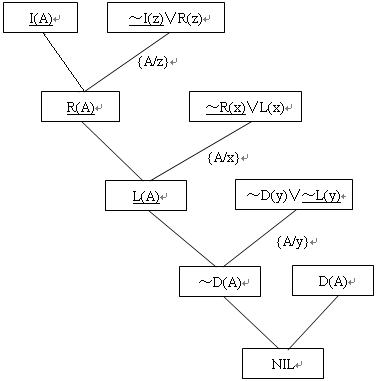
（5）R（A） （3b）和（4）的归结式
（6）L（A） （5）和（1）的归结式
（7）~D（A） （6）和（2）归结式
（8）NIL （7）和（3a）的归结式