在谓词逻辑的归结过程中，寻找项之间合适的变量置换使表达式一致是一个很重要的过程，这个过程称为合一。下面先讨论置换的几个概念，然后再给出合一算法。
　　一个表达式的项可以是常量符号、变量符号或函数式（由函数符号及其项组成）。表达式的例（instance）是指在表达式中用置换项置换变量后而得到的一个特定的表达式。例如表达式P[x，f（y），B]，对应于不同的变换si，可得到不同的例：

第一个例叫做原始文字的初等变式，实际上置换后只是对变量作了换名。而第四个例称作基例，即置换后项中不再含有变量。
通常用有序对的集合来表示任一置换，用s对表达式E作置换后的例简记为Es。置换集的元素的含义是表达式中的变量vi处处以项ti来替换，但不允许vi用与vi有关的项作置换。
有时候要对表达式多次置换，如用s1，s2依次进行置换（即（Es1）s2），这时可以将这两个置换合成为一个置换（记为s1s2）。合成置换s1s2是由两部分的置换对组成：一部分仍是s1的换对，只是s1的项被s2作了置换；另一部分是s2中与s1变量不同的那些变量对。例如
s1＝{g（x，y）/z}，s2＝{A/x，B/y，C/w，D/z}
s1s2＝{g（A，B）/z，A/x，B/y，C/w}
这样的合成法可使（Es1）s2＝E（s1s2），这表明置换的合成是可以结合的，但很容易检验出，一般情况下置换是不可交换的，即。
若存在一个置换s使得表达式集{Ei}中每个元素经置换后的例有：，则称表达式集{Ei}是可合一的，这个置换s称作{Ei}的合一者。在归结法中主要是处理可合一的子句集，例如有子句集{P（x，f（y），B），P（x，f（B），B）}，若对两个子句作置换s＝{A/x，B/y}，则可得{P（A，f（B），B）}，因而该子句集是可合一的。
仅仅从合一的角度看，s并不是最简单的合一者，因为还存在另一个s1＝{B/y}的合一者，使子句集合一为{P[x，f（B），B]}。因此通常还要求找的是最一般或最普通的合一者（most general unifier）g，记为mgu g。
任一合一者s与g之间的关系是：存在一个置换s′，使得{Ei}s＝{Ei}gs′。再比较上例的两个合一者，有{A/x，B/y}＝{B/y}{A/x}，因此mgu g＝{B/y}。可见mgu g的置换限制最少，所产生的例更一般化，这有利于归结过程的灵活使用。

　　UNIFY算法不仅可以判断两个公式是否可合一，而且在可合一的情况下，给出它们的mgu。该算法为了表述上的方便，假定谓词是以表的形式表示的。如谓词P(x, f(y), B)表示为(P x (f y) B)。
　　UNIFY算法是用递归的方法描述的，如果对递归不熟悉，请参看第二章中回溯算法中对递归的介绍。
　　UNIFY算法的基本思想是，从左向右按位置扫描两个谓词的每一个对应部分，如果二者一致，则转入下一项。如果不一致，则看是否存在一个置换，使得对应项经过置换后是一致的。如果不存在这样的置换，则两个公式是不可合一的。如果两个谓词的对应部分都是一致的，或者经置换后是一致的，则两个公式是可合一的，这些置换的合成是它们的合一者。如果当两个对应项都是变量时，置换选作用一个变量代替另一个变量，则这样得到的合一者是mgu。
　　该算法描述适合于程序实现，并不太适合于人的操作。下面通过一个例子，来说明如何判断两个公式是否可合一以及如何求mgu。其过程与UNIFY算法的思想是一致的。
例：
公式集如下：
{P(x, x, z), P(f(y), f(B), y)}
用表的形式表示为：
E1=(P x x z)
E2=(P (f y) (f B) y)
为清楚起见，两个谓词按位置上下对齐。
从左向右按顺序扫描两个谓词。E1和E2的第一项都是P，是一致的，转入第二项。E1的第二项是x，E2的第二项是(f y)，二者不一致。由于其中一个是变量，可以进行置换。选置换{(f y)/x}使得二者成为一致的。该置换同时作用于E1的第三项x。这样有：
E1= (P (f y) (f y) z)
E2= (P (f y) (f B) B)
继续看第三项。E1的第三项是(f y)，E2的第三项是(f, B)。由于两个都是表，需要进入表的内部进行比较。
在表的内部，第一项均是f，是一致的。第二项一个是变量y，一个是常量B。选置换{B/y}使二者成为一致的。该置换不仅使得两个公式中的所有y都被替换为了B，而且也作用于前一个置换{(f y)/x}，使得该置换变成了{(f B)/x}。这样有：
E1= (P (f B) (f B) z)
E2= (P (f B) (f B) B)
E1的第四项是变量z，E2的第四项是常量B，选置换{B/z}使得二者成为一致的。有：
E1= (P (f B) (f B) B)
E2= (P (f B) (f B) B)
至此，E1和E2是完全一样的了，说明E1和E2是可合一的。其合一者是这一过程中几个置换的并{(f B)/x, B/y, B/z}，该合一者也是mgu。
如果这一过程中有某一个对应项是不能置换为一样的，则说明两个公式不可合一。如该例如果是：
E1=(P x x A)
E2=(P (f y) (f B) y)
则是不可合一的。因为经过几步变换后有：
E1= (P (f B) (f B) A)
E2= (P (f B) (f B) B)
此时E1的第四项是常量A，而E2的第四项是常量B，二者不一致，而且都是常量，无法置换。因此两个公式不可合一。

下面给出UNIFY算法，要注意算法中可合一的表达式要用表结构来表示，如把P（x，f（A，y））表示成（P x （f A y））。找到的合一者是可合一表达式的mgu，若表达式不可合一时，则算法失败退出。

UNIFY算法判断两个公式E1和E2是否可合一。当可合一时，返回它们的mgu，否则返回FAIL。

递归过程UNIFY（E1，E2）

当E为原子时，ATOM为真，否则为假。由于合适公式已经用表的形式表示，所以在这里谓词符号、函数符号、常量、变量、否定符号等，均为原子。
①IF ATOM（E1） OR ATOM（E2）
　　THEN 交换E1和E2的位置使E1是一个原子（有必要时），do： ；原子包括谓词符号、函数符号、常数符号、变量符号和否定符号。E1不是原子，而E2是原子时，则交换位置，使E1是一个原子。
②begin
③ IF E1＝E2 THEN RETURN NIL；

　　当E为变量时，VAR(E)为真，否则为假。当E2中含有E1时，CONTAIN（E2，E1）为真，否则为假。当E2中含有E1时，也就是类似于x与(f x)进行合一这样的情形出现时，由于会产生无穷的嵌套，因此合一失败。

④ IF VAR（E1）IF CONTAIN （E2，E1）THEN RETURN（FAIL） ELSE RETURN （{E2/E1}）；E1是变量且E2中不含有E1，返回置换{E2/E1}。
⑤ IF VAR（E2） THEN RETURN （{E1/E2}）
ELSE RETURN （FAIL）；E2是变量返回置换{E1/E2}。
⑥end

FIRST表示取一个表的第一个元素。如FIRST((a b c))＝a，FIRST((a b) c d)＝(a b)。TAIL表示取一个表的尾，也就是说去掉表的第一个元素后得到的表。如TAIL((a b c))=(b c)，TAIL((a b) c d)=(c d)。

利用该算法可找到可合一表达式集的最一般的合一者，下面给出几个可合一集得到的结果。

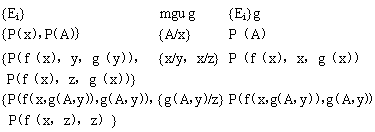
　　合一算法是解决两个表达式匹配的问题，两个表达式都可以含有变量，通过算法求得mgu并进行置换后就可以得到匹配的例。在人工智能中所谓的模式匹配是一个表达式同另一个模式表达式匹配的过程，和合一过程有类似之处，只是模式匹配过程不允许变量同时出现在两个表达式中。