（2）命题逻辑的归结过程
　　命题逻辑中，若给定公理集F和命题P，则归结证明过程可归纳如下：
①把F转化成子句集表示，得子句集S0；
②把命题P的否定式~P也转化成子句集表示，并将其加到S0中，得S＝S0∪{S~p}；
③对子句集S反复应用归结推理规则，直至导出含有空子句的扩大子句集为止。即出现归结式为空子句的情况时，表明已找到了矛盾，证明过程结束。

将所有的已知条件和结论的否定"与"在一起求子句集和对每个已知条件及结论的否定分别求子句集，再将分别得到的子句集并在一起得到的子句集是一样的。
对于该例，由（1）有子句集{P}；
由（2）有：
（P∧Q）→R
＝> ～(P∧Q)∨R
＝> (～P∨～Q∨R)
得子句集：{～P∨～Q∨R}
由（3）有：
(S∨T)→Q
＝> ～(S∨T)∨Q
＝> (～S∧～T)∨Q
＝> (～S∨Q)∧(～T∨Q)
得子句集：{～S∨Q, ～T∨Q}
有（4）有子句集：(T)。
由结论的否定得子句集：{～R}
将以上子句集并在一起有总的子句集：
{P，~P∨~Q∨R，~S∨Q，~T∨Q，T，~R}
归结的结果如图4.1所示。注意，这一归结过程并不是唯一的，选择不同的归结对进行归结，将得到不同的归结过程。

例：设已知公理集为
P………………… （1）
（P∧Q）→R……（2）
（S∨T）→Q……（3）
T…………………（4）
求证R。
化成子句集表示后得
S＝{P，~P∨~Q∨R，~S∨Q，~T∨Q，T，~R}

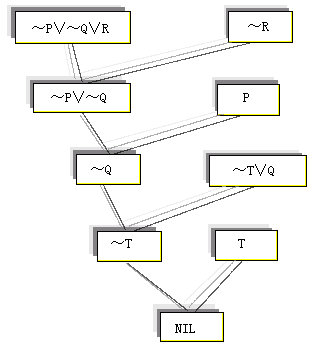
图4.1 命题逻辑的归结演绎树

　　归结过程很简单，可用图4.1的演绎树表示，由于根部出现空子句，因此命题R得到证明。
　　这个归结法证明过程其意义可解释如下：一开始是假设S集中所有的子句均为真，而生成的归结式表示由其他某个子句提供的信息使S中原子句为真的限制条件。当某一个子句限制太多时，可能就无法保证它为真了，这时就会出现矛盾，空子句就代表矛盾的出现。具体来说，要命题（2）为真，~P，~Q或R中应有一个为真，导出第一个归结式时已假定~R为真，因此命题（2）为真就要受到限制，只能是~P或~Q有一个为真。而当导第二个归结式时，已知命题P为真，因此命题（2）为真的条件进一步限制为~Q为真了。同理导第三个归结式时，可得出命题（3）的分命题~T∨Q为真的限制是~T为真，但命题（4）言称T必为真，这就导致了矛盾的出现，产生了空子句，说明无法使S中所有子句在某一解释下均为真。结论是因命题（1）-（4）均为真，所以只能~R为假了。

　　3．谓词逻辑的归结原理

　　在命题逻辑中，比较容易确定用于归结的两个归结对。而对于谓词逻辑来说，由于谓词具有常量、变量和函数等变元的存在，两个子句是否可用于归结，判断起来就有些复杂。比如：子句P(x)∨Q(y)和子句～P(f(y))∨R(y)是否可以进行归结呢？子句P(A)∨Q(y)和子句～P(f(y))∨R(y)又如何呢？在后边我们将会看到，前者是可以进行归结的，而后者则不可以。如果两个子句可以进行归结，那么其归结式又是怎样的呢？这里首先要涉及合一的概念。

　　从命题逻辑的归结过程中看出，求归结式时比较容易确定含有互补对文字的两个子句，这只要检查一下L和~L就可以了，因而匹配过程比较简单。而在谓词逻辑中，由于要考虑变量的约束问题，这一匹配过程就复杂多了，因而在应用归结法时，往往要对公式作变量置换和合一等处理，才能得到互补的基本式，以便进行归结。因此谓词逻辑的归结过程是：
・若S中两子句间有相同互补文字的谓词，但它们的项不同，则必须找出对应的不一致项；
・进行变量置换，使它们的对应项一致；
・求归结式看能否导出空子句。
下面进一步讨论合一和归结过程。
（1）合一（Unify）

一个有序对的集合s={ti/vi}（i=1, 2,…, n）称为置换。其中vi（i=1, 2, ... n）是变量，ti（i=1, 2, ... n）是不同于vi的项，可以是常量、函数，或者其他的变量。置换s表示将公式（表达式）中的所有变量vi用项ti代替。对公式E施以置换s，记作Es。Es称作公式E的例。
例：
设有置换s={z/x, A/y}，
则：P[x, f(y), B]s=P[z, f(A), B]。
这里x被换成了z，y被换成了A。
设有公式的集合{Ei}(i=1, 2, ..., m)，如果存在一个置换s，使得这m个公式被施以s以后，变得完全一样了，则称这m个公式是可合一的，置换s是它们的合一者。
例：
设有公式集{P(x, f(y), B), P(z, f(B), B)}和置换s1={A/x, B/y, A/z}，由于：
P(x, f(y), B)s=P(A, f(B), B)
P(z, f(B), B)s=P(A, f(B), B)
所以公式集{P(x, f(y), B), P(z, f(B), B)}是可合一的，置换s1={A/x, B/y, A/z}是它们的合一者。
一般来说，一个公式集的合一者不是唯一的。如s2={z/x, B/y}和s3={x/z, B/y}都是公式集{P(x, f(y), B), P(z, f(B), B)}的合一者。
对于一个公式集来说，如果存在几个合一者，则其中置换数最少、限制最少、产生的例最具一般性的置换称为最一般合一者（mgu）。
如在上例中，置换s1={A/x, B/y, A/z}产生的例为P(A, f(B), B)，置换s2={z/x, B/y}产生的例为P(z, f(B), B)。对于置换s1，置换数为3，而置换s2的置换数为2。相对于例P(A, f(B), B)来说，例P(z, f(B), B)含有一个变量，因此更具一般性。实际上置换s2就是上例公式集的最一般合一者，即mgu。置换s3={x/z, B/y}也是该公式集的mgu。可见mgu也同样不是唯一的。