3．极小极大搜索过程
　　极小极大搜索方法是博弈树搜索的基本方法，现在博弈树搜索中最常用的α-β剪枝搜索方法，就是从这一方法发展而来的。
　　首先假定，有一个评价函数可以对所有的棋局进行评估。当评价函数值大于0时，表示棋局对我方有利，对对方不利。当评价函数小于0时，表示棋局对我方不利，对对方有利。而评价函数值越大，表示对我方越有利。当评价函数值等于正无穷大时，表示我方必胜。评价函数值越小，表示对我方越不利。当评价函数值等于负无穷大时，表示对方必胜。假设双方都是对弈高手，在只看一步棋的情况下，我方一定走评价函数值最大的一步棋，而对方一定走评价函数值最小的一步棋。会下棋的读者都知道，在只看一步的情况下最好的棋，从全局来说不一定就好，还可能很不好。因此为了走出好棋，必须多看几步，从多种可能状态中选择一步好棋。
　　想一想人是如何下棋的呢？人实际上采用的是一种试探性的方法。首先假定走了一步棋，看对方会有那些应法，然后再根据对方的每一种应法，看我方是否有好的回应......这一过程一直进行下去，直到若干步以后，找到了一个满意的走法为止。初学者可能只能看一、两个轮次，而高手则可以看几个，甚至十几个轮次。
　　极小极大搜索方法，模拟的就是人的这样一种思维过程。当轮到我方走棋时，首先按照一定的搜索深度生成出给定深度d以内的所有状态，计算所有叶节点的评价函数值。然后从d-1层节点开始逆向计算：对于我方要走的节点（用MAX标记，称为极大节点）取其子节点中的最大值为该节点的值（因为我方总是选择对我方有利的棋）；对于对方要走的节点（用MIN标记，称为极小节点）取其子节点中的最小值为该节点的值（对方总是选择对我方不利的棋）。一直到计算出根节点的值为止。获得根节点取值的那一分枝，即为所选择的最佳走步。
　　在图3.5所示的例子中，假定搜索深度为2，D～J是7个叶节点，在它们下边括号中的数字是这些节点的评价函数值（假定可以计算得到）。A、B、C是三个极小节点，它们分别取各自子节点最小值为自己的值，得到三个节点的值分别为-6、-2和-4。s是极大节点，从A、B、C三个节点的值中取最大值，得到-2。由于-2来自于节点B，所以搜索的结果是应选择B作为我方的走步。对于我方来说，-2并不是一个好的结果，但却是在对方不犯错误的情况下，对我方最有利的结果。因为从图中可以看出，如果选择A为我方的走步，如果对方回应D的话，我方可以得到评价值9，固然对我方有利。但是如果对方是一个高手的话，他一定回选择E，而不是D。在这种情况下，我方只能得到-6，结果岂不是更差。因此，极小极大过程是一种假定对手每次回应都正确的情况下，如何从中找出对我方最有利的走步的搜索方法。
　　值得注意的是，不管设定的搜索深度是多少层，经过一次搜索以后，只决定了我方一步棋的走法。等到对方回应一步棋之后，需要在新的棋局下重新进行搜索，来决定下一步棋如何走。

　　极小极大搜索策略是考虑双方对弈若干步之后，从可能的走步中选一步相对好棋的着法来走，即在有限的搜索深度范围内进行求解。为此要定义一个静态估计函数f，以便对棋局的势态（节点）作出优劣估值，这个函数可根据势态优劣特征来定义（主要用于对端节点的"价值"进行度量）。一般规定有利于MAX的势态，f（p）取正值，有利于MIN的势态，f（p）取负值，势均力敌的势态，f（p）取0值。若f（p）＝＋∞，则表示MAX赢，若f（p）＝－∞，则表示MIN赢。下面的讨论规定：顶节点深度d＝0，MAX代表程序方，MIN代表对手方，MAX先走。
　　图3.5是一个表示考虑两步棋的例子，图中端节点给出的数字是用静态函数f（p）计算得到，其他节点不用f（p）估计，因为不够精确，而应用倒推的办法取值。例如A、B、C是MIN走步的节点，MAX应考虑最坏的情况，故其估值应分别取其子节点f（p）估值中最小者，而s是MAX走步的节点，可考虑最好的情况，故估值应取A、B、C值中的最大者。这样求得f（s）＝－2，依此确定了相对较优的走步应是走向B，因为从B出发，对手不可能产生比f（s）＝－2更差的效果。实际上可根据资源条件，考虑更多层次的搜索过程，从而可得到更准确的倒推值，供MAX选取更正确的走步。当用端节点的静态估计函数f（p）求倒推值时，两位选手应采取不同的策略，从下往上逐层交替使用极小和极大的选值方法，故称极小极大过程。

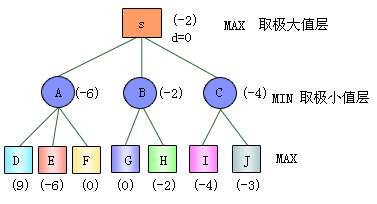
图3.5 f(p)求值过程

过程MINIMAX：
①T:＝（s，MAX），OPEN:＝（s），CLOSED:＝（ ）；开始时树由初始节点构成，OPEN表只含有s。
②LOOP1:IF OPEN＝（ ）THEN GO LOOP2；
③n:＝FIRST（OPEN），REMOVE（n，OPEN），ADD（n，CLOSED）；
④IF n可直接判定为赢、输或平局
THEN f（n）:＝∞∨－∞∨0，GO LOOP1
ELSE EXPAND（n）→{ni}，ADD（{}，T）
IF d（ni）＜k THEN ADD（{}，OPEN），GO LOOP1
ELSE计算f（），GO LOOP1；nI达到深度k，计算各端节点f值。
⑤LOOP2：IF CLOSED＝NIL THEN GO LOOP3
ELSE :＝FIRST（CLOSED）；
⑥IF（∈MAX）∧（f（∈MIN）有值）
THEN f（）:＝max{f（）}，REMOVE（，CLOSED）；若MAX所有子节点均有值，则该MAX取其极大值。
IF （∈MIN）∧（f（∈MAX）有值）
THEN f（）:＝min{f（）}，REMOVE（，CLOSED）；若MIN所有子节点均有值，则该MIN取其极小值。
⑦GO LOOP2；
⑧LOOP3：IF f（s）≠NIL THEN EXIT（END∨M（Move，T））；s有值，则结束或标记走步。
该算法分两个阶段进行，第一阶段②-④是用宽度优先法生成规定深度的全部博弈树，然后对其所有端节点计算其静态估计函数值。第二阶段⑥-⑧是从底向上逐级求非端节点的倒推估计值，直到求出初始节点的倒推值f（s）为止，此时

其中 表示深度为k的端节点。再由f（s）即可选得相对较好的走步来，过程遂造结束。等对手响应走步后，再以当前的状态作为起始状态s，重复调用该过程。
下面通过最简单的3×3棋盘的一字棋为例来说明算法的应用过程。
在九宫格棋盘上，两位选手轮流在棋盘上摆各自的棋子（每次一枚），谁先取得三子一线的结果就取胜。
设程序方MAX的棋子用（×）表示，对手MIN的棋子用（○）表示，MAX先走。静态估计函数f（p）规定如下：
若p对任何一方来说都不是获胜的格局，则
f（p）＝（所有空格都放上MAX的棋子之后，MAX的三子成线（行、列、对角）的总
－（所有空格都放上MIN的棋子之后，MIN的三子成线（行、列、对角）的总数）
若p是MAX获胜的格局，则f（p）＝∞；
若p是MIN获胜的格局，则f（p）＝－∞。
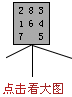
例如，当p的格局如下时，则可得f（p）＝6－4＝2；

　　设考虑走两步的搜索过程，利用棋盘对称性的条件，则第一次调用算法产生的搜索树如图3.6所示，图中端节点下面是计算的f（p）值，非端节点的倒推值标记在圆圈内。为了使初始节点具有最大的倒推值，可以看出第一步的最好着法是把棋子下在中央位置。

图3.6一字棋第一阶段搜索树

设MAX走完第一步后，MAX的对手是在×之上的格子下子，这时MAX就要在新格局下调用算法，第二次产生的搜索树如图3.7所示。类似的第三次的搜索树如图3.8所示。至此MAX走完最好的走步后，不论MIN怎么走，都无法挽回败局，因此只好认输了，否则还要进行第四轮回的搜索。

图3.7 一字棋第二阶段搜索树

图3.8一字棋第三阶段搜索树