3.3 博弈树的搜索

　　 1．概述
　　博弈一向被认为是富有智能行为的游戏，因而很早就受到人工智能界的重视，早在60年代就已经出现若干博弈程序，并达到一定水平。博弈问题的研究还不断提出一些新的研究课题，从而也推动了人工智能研究的发展。
　　对于单人博弈的一些问题，可用一般的搜索技术进行求解，本节着重讨论双人完备信息这一类博弈问题的搜索策略。由于双人博弈可用与或树（或图）来描述，因而搜索就是寻找最佳解树（图）的问题。
　　所谓双人完备信息，就是两位选手对垒，轮流走步，这时每一方不仅都知道对方过去已经走过的棋步，而且还能估计出对方未来可能的走步。对弈的结果是一方赢（另一方则输），或者双方和局。这类博弈的实例有：一字棋、余一棋、西洋跳棋、国际象棋、中国象棋、围棋等。对于带机遇性的任何博弈，因不具有完备信息，不属这里讨论范围，但有些论述可推广到某些机遇博弈中应用。
　　博弈问题可以用产生式系统的形式来描述，例如中国象棋，综合数据库可规定为棋盘上棋子各种位置布局的一种描述，产生式规则是各类棋子合法走步的描述，目标则可规定为将（帅）被吃掉，规则作用于数据库的结果便生成出博弈图或博弈树。下面举一个简单的例子说明博弈问题可用与或图表示，并讨论搜索策略应考虑的实际问题。

　　2．Grundy博弈
　　分钱币问题是一种简单的博弈问题。对于这样的简单博弈问题，可以生成出它的状态空间图。这样就有可能从状态空间图中找出取胜的策略。图3.4给出的就是当初始钱币数为7时的状态空间图，其中MIN代表对方走，MAX代表我方走。从图中可以看出，在第一轮次对方一共有三种可能的走法，而不管对方如何走，我方都可以走到（4，2，1，MIN）这个状态。对方只能走到（3，2，1，1，MAX）。而这时我方走到（2，2，1，1，1，MIN）就获胜了。所以，对于这样一个分钱币问题，后走者总是能够获胜的。
　　对于简单问题可以这样找到取胜策略，但对于复杂问题就不可能了。以中国象棋为例，其全部状态数平均大约是10161个。有人测算过，即便用当前最快的计算机来生成这些状态，所用的时间大约比宇宙的年龄还长。因此，对于实际的博弈问题，无论是从空间，还是从时间上来说，要想通过生成其所有状态空间图的方法来得到取胜策略，都是不可能的。下面所要讨论的，就是如何根据有限的状态，得到较好走步的搜索方法。也就是说，通过看若干步以后的棋局情况，选择出比较佳的走步。

Grundy博弈是一个分钱币的游戏。有一堆数目为N的钱币，由两位选手轮流进行分堆，要求每个选手每次只把其中某一堆分成数目不等的两小堆。例如选手甲把N分成两堆后，轮到选手乙就可以挑其中一堆来分，如此进行下去直到有一位选手先无法把钱币再分成不相等的两堆时就得认输。

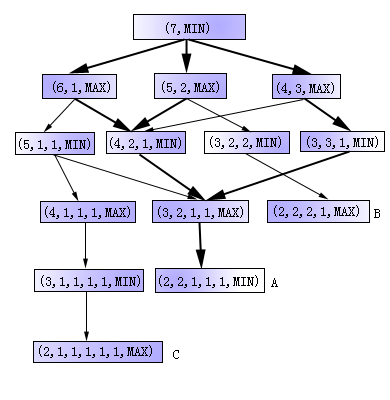
图3.4 Grundy博弈状态空间图

　　分钱币问题的产生式系统描述：
　　综合数据库：用无序数字序列x1，x2，…，表示n堆钱币不同的个数，再用两个说明符号代表选手，无序数列和符号M组合（x1，x2，…，，M）就代表由某个选手走步的状态。
规则：if （x1，…，，M）∧（xj＝y+z，y≠z）
then （x1，…，，y，z，，…，xn，）
　　设初始状态为（7，MIN），则该问题的状态空间图如图3.4所示，图中所有终节点均表示该选手必输的情况，取胜方的目标是设法使棋局发展为结束在对方走步时的终节点上，因此节点A是MAX的搜索目标，而节点B，C则为MIN的搜索目标。
　　搜索策略要考虑的问题是：
　　对MIN走步后的每一个MAX节点，必须证明MAX对MIN可能走的每一个棋局对弈后能获胜，即MAX必须考虑应付MIN的所有招法，这是一个与的含意，因此含有MAX符号的节点可看成与节点。
　　对MAX走步后的每一个MIN节点，只须证明MAX有一步能走赢就可以，即MAX只要考虑能走出一步棋使MIN无法招架就成，因此含有MIN符号的节点可看成或节点。
　　这样一来对弈过程的搜索图就呈现出与或图表示的形式，从搜索图中可以看出，MAX存在完全取胜的策略，图中粗线所示部分就代表了这种策略，这时不论MIN怎么走，MAX均可取胜。因而寻找MAX的取胜策略便和求与或图的解图一致起来，即MAX要取胜，必须对所有与节点取胜，但只需对一个或节点取胜，这就是一个解图。因此实现一种取胜的策略就是搜索一个解图的问题，解图就代表一种完整的博弈策略。
　　对于Grundy这种较简单的博弈，或者复杂博弈的残局，可以用类似于与或图的搜索技术求出解图，解图代表了从开局到终局任何阶段上的弈法。显然这对许多博弈问题是不可能实现的。例如中国象棋，每个势态有40种不同的走法，如果一盘棋双方平均走50步，则搜索的位置有，即深度达100层，总节点数约为个。因此要考虑完整的搜索策略，就是用亿次机来处理，也得花天文数字计的时间。对于西洋跳棋、国际象棋大致也如此，而围棋更复杂了。因此即使用了强有力的启发式搜索技术，也不可能使分枝压到很少，因此这种完全取胜策略（或和局）必须丢弃，而应当把目标确定为寻找一步好棋，等对手回敬后再考虑寻找另一步好棋这种实际可行的实用策略。这种情况下每一步结束条件可根据时间限制、存储空间限制或深度限制等因素加以确定。搜索策略可采用宽度、深度或启发式方法，一个阶段搜索结束后，要从搜索树中提取一个优先考虑的"最好的"走步，这就是实用策略的基本点。下面就来讨论这种机理的搜索策略--极小极大搜索过程。