应用算法求解，经过4个大循环后就找到解图，图3.3给出这4个循环之后的搜索结果。第四个循环后算法结束，这时带指针的连接符就给出了所得到的解图，n0给出的修正耗散值q（n0）＝5就是解图的实际耗散值。该例中显然找到了具有最小耗散值的解图。

3．算法应用的若干问题

（1）在第6步扩展节点n时，若不存在后继节点（即陷入死胡同），则可在第11步中对m（即n）赋一个高的q值，这个高的q值会依次传递到s，使得含有节点n的子图具有高的q（s），从而排除了被当作候选局部解图的可能性。

　　算法的第五步，从G′中选择一个非终节点扩展。一般情况下会有若干个非终节点供选择，算法并没有规定选择节点的方式。如果最终求解出来的解图是从该G′产生的，则优先选择哪个节点先扩展并不重要，因为这几个节点最终都要被扩展的，扩展次序的先后，并不会影响到搜索的效率。我们考虑最终的解图不是从该G′产生的情况。则在这种情况下，如果问题有解的话，最佳解图应从其他的局部图产生。所以此时应该尽快从G′中跳出来，转到别的局部图去搜索。而跳出G′的唯一条件是使得G′的耗散值不是最小。假设G′有两个非终节点，一个h值小，一个h值大。显然先扩展h值大的节点会有力于尽快从G′中跳出。因此，当有几个非终节点供选择时，选择h值较大的节点首先扩展，有利于提高搜索的效率。

（2）第5步中怎样选出G′中的一个非终节点来扩展呢？一般可以选一个最可能导致该局部解图耗散值发生较大变化的那个节点先扩展，因为选这个节点先扩展，会促使及时修改局部解图的标记。

与A*算法不同的是，只有当h满足单调限制条件时，AO*才能够在问题有解的情况，一定保证找到最佳解图。

（3）同A算法类似，若s→N集存在解图，当h（n）≤h*（n）且h（n）满足单调限制条件时，则AO*一定能找到最佳解图，即AO*具有可采纳性。当h（n）≡0时，AO*也蜕化为宽度优先算法。
这里单调限制条件是指：对隐含图中，从节点n→{n1，…，nk}的每一个连接符都施加限制，即假定h（n）≤C+h（n1）+…+h（nk）其中C是连接符的耗散值。
如果h（n）满足单调限制，且h（ti）＝0（ti∈N），那么单调限制意味着h是h*的下界范围，即对所有节点n有h（n）≤h*（n）。

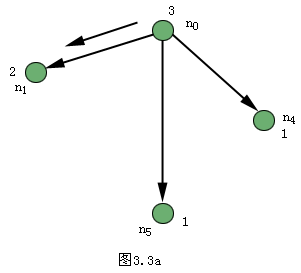
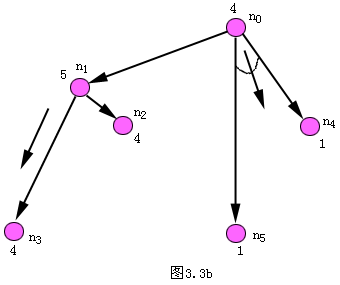
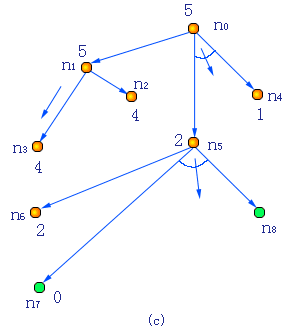
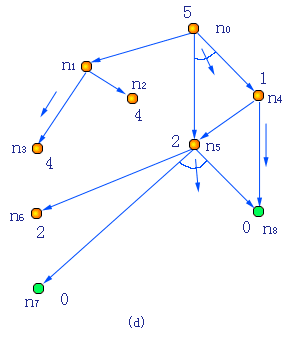
图3.3 AO*算法4个循环的搜索图
（a）一次循环之后（b）两次循环之后
（c）三次循环之后（d）四次循环之后

　　综上所述，看出与A有类似之处，但也有若干区别。首先是AO*算法不能像A算法那样，单纯靠评价某一个节点来评价局部图。其次是由于k-连接符连接的有关子节点，对父节点能解与否以及耗散值都有影响，因而显然不能象A算法那样优先扩展其中具有最小耗散值的节点。再一点是算法仅适用于无环图的假设，否则耗散值递归计算不能收敛，因而在算法中还必须检查新生成的节点已在图中时，是否是正被扩展节点的先辈节点。最后还必须注意A算法没有OPEN和CLOSED表，而AO*算法只用一个结构G，它代表到目前为止已明显生成的部分搜索图，图中每一个节点的h（n）值是估计最佳解图，而不是估计解路径。
　　有关AO*算法的具体应用及一些提高搜索效率的修正算法，可进一步参阅人工智能有关文献。