2．算法应用举例

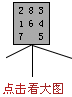
　　设某个问题的状态空间如图3.1所示，并定义了某个启发函数h（n），我们来看一看解图的搜索过程。
　　为了使用方便，将h（n）函数对图3.1中各节点的假想估值先列写如下（实际应用中是节点生成出来之后才根据h（n）定义式计算）：
h（n0）＝3，h（n1）＝2，h（n2）＝4，h（n3）＝4，h（n4）＝1，h（n5）＝1，h（n6）＝2，h（n7）＝h（n8）＝0（目标节点）。
此外我们假设k-连接符的耗散值为k。

图3.3给出了使用算法对图3.1所示与或图的搜索过程。
　　开始时，只有一个初始节点n0，n0被扩展，生成出节点n1、n4和n5，一个1－连接符指向n1，一个2－连接符指向n4和n5。这两个连接符之间是"或"的关系。由已知条件知：h(n1)=2，h(n4)=1，h(n5)=1，并且已经假设k－连接符的耗散值为k。所以由n0的1－连接符，可以计算出n0的耗散值（即算法中的q值，为了与算法一直，以下用q值表示）为（n0的1－连接符的耗散值）＋（n1的q值）＝1＋2＝3。对于目前得到的局部图来说，n1是一个叶节点，所以其q值用h值（＝2）代替。由n0的2－连接符，可以计算出n0的q值为（n0的2－连接符的耗散值）＋（n4的q值）＋（n5的q值）＝2＋1＋1＝4。在两个不同渠道计算得到的耗散值中取最小值作为n0的q值，并设置一个指针指向提供该耗散值的连接符。在这里3<4，所以n0的q值为3，指针所指向的连接符为n0的1－连接符。至此算法的第一个循环结束。搜索图如图3.3（a）所示。
　　在第二个循环中，首先从n0开始，沿指针所指向的连接符，寻找一个未扩展的非终节点。这时找到的是n1节点。扩展n1节点，生成出节点n2和n3，两个节点分别通过1－连接符与n1连接。由于h(n2)=h(n3)=4，所以通过这两个连接符计算的耗散值也一样，均为5。取其最小者还是5，从而更新n1的q值为5。由于耗散值相等，所以指向连接符的指针可以指向两个连接符中的任何一个，假定指向了n3这一边。由于n1的q值由2更新为5，所以需要从新计算n0的q值。对于n0来说，此时从1－连接符这边算得的耗散值为6，大于从2－连接符这边得到的耗散值4，所以n0的q值更新为4，并将指向连接符的指针由指向1－连接符改为指向2－连接符。注意，这时由n1出发的指向连接符的指针并没有被改变或删除。至此第二循环结束，搜索图如图3.3（b）所示。
　　在第三个循环中，同样从n0开始，沿指针所指向的连接符，寻找未扩展的非终节点。这时n4和n5都是满足这一条件的节点，可以从它们中任选择一个扩展。假定选择的是n5。n5生成出n6、n7和n8三个节点。一个1－连接符指向n6，一个2－连接符指向n7和n8。计算的结果，得到n5的q值为2，指针指向2－连接符。由于n5的q值改变了，因此需要重新计算n0的q值，计算的结果为5。该结果还是比通过n0的1－连接符计算得到的耗散值小，因此只需更新n0的q值即可，不需要改变指向连接符的指针。
　　在本次循环中，由于n7和n8都是目标节点，是能解节点，而n5通过一个2－连接符连接n7和n8，所以n5也被标记为能解节点。虽然n5是能解节点，但由于n0是通过一个2－连接符连接n5和n4，而此时n4还不是能解的，所以n0还不是能解的。搜索将继续进行。至此第三循环结束，搜索图如图3.3（c）所示。
　　第四次循环，同样的道理，从n0开始沿指针所指向的连接符，寻找未扩展的非终节点，这次找到的是n4。扩展n4，生成节点n5和n8，并分别以1－连接符连接。对n4来说，从n5这边计算得耗散值为3（n5已经被扩展过，其q值已经被更新为2，因此在计算n4的耗散值时，应使用更新后的q值，而不是n5的h值），从n8这边计算得耗散值为1。取小者，得n4的q值为1，并且将指向连接符的指针指向n8这边的连接符。因为扩展n4并没有改变它的q值，因此n0的q值也不需重新计算了。由于n8是目标节点，是能解节点，而n4通过一个1－连接符连接n8，因此n4也被标记为能解节点。在第三循环中，n5已经被标记为能解节点。这样n4、n5都是能解节点了，从而n0也被标记为能解节点。而n0是初始节点，至此搜索全部结束。从n0开始，沿指向连接符的指针找到的解图即为搜索的结果。下图为得到的解图。

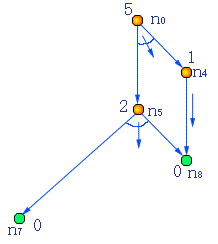
搜索得到的解图