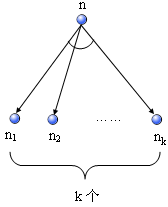
在现实世界中，经常会遇到这样的问题：一个问题可以有几种求解方法，只要其中一种方法可以求解问题，则该问题被求解。也就是说，对求解该问题来说，方法之间是"或"的关系。但在用每一种方法求解时，又可能需要求解几个子问题，这些子问题必须全部求解，才可能用该方法求解原始问题。也就是说，这些子问题之间是"与"的关系。此类问题可以用与或图来表示。图3.1是一个与或图的示例。它表示，如果要求解n0，可以求解n1，或者求解n4、n5，也就是说，对于n0来说，n4和n5是"与"的关系，而n1和n4、n5的"与"之间是"或"的关系。其他节点之间也具有类似的关系。一个节点与它的k个与子节点间用下图的形式连接，称为k－连接符。

　　可分解产生式系统中提到的与或树表示，其中加到每一个节点上"与"或"或"的标记是取决于该节点对其父节点的关系。如复合数据库分解后拥有一组"与"关系的后继节点；而分量数据库经可应用规则作用后，生成一组"或"关系的后继节点。
　　通常我们要讨论与或图的一般情况（与或树是其特例），即应用不同的规则序列可能会生成出相同的数据库。例如某一个分量数据库标记的节点，可以是某一个已被分解的复合数据库的一个子节点，应称它为"与"节点；但这个分量数据库标记的节点也可以是另一个分量数据库使用某一规则之后得到的子节点，那么它又是"或"节点。为了避免混淆不清，通常不把与或图中节点叫做与节点或者或节点，而是引入一个适合于与或图的更一般的标记，而在称谓上沿用习惯，仍把这种结构称作与或图。当然在讨论与或树时仍继续用"与"、"或"节点的称呼。
　　图3.1给出一个简单的与或图例子，下面就来说明它的标记方法。

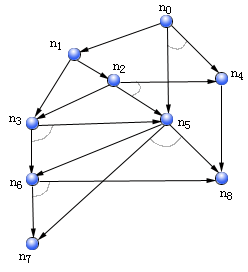
图3.1与或图

　　这个图也称做超图，节点间是用超弧线（或连接符）来连接，如一个父节点和一组后继节点的关系可用若干个连接符来标记，并规定k-连接符是从一个父节点指向一组k个后继节点的节点集。这时若节点间全是1-连接符（相当于一条弧线）连接，显然这就是一般图的标记法，得到的就是与或图的特例--普通图。
　　从图3.1可以看出，节点n0有两个连接符：1-连接符指向节点n1；2-连接符指向节点集{n4，n5}。该2-连接符还用一小段圆弧括起来（对k＞1的k-连接符都应有小圆弧标记），以表示子节点间与的关系。可以看出这种标记法在节点间具有明确的关系。显然若用原先的术语，则对父节点n0来说，n4、n5是两个与节点，而n1可称为或节点；而n8既是n5的一个与节点，又是n4的一个或节点，混淆难于避免。另外也把图中没有任何父节点的节点叫根节点，没有任何后继节点的节点叫端节点或叶节点。
　　一个可分解产生式系统规定了一个隐含的与或图，初始数据库对应于图中的初始节点，它有一个外向的连接符连到它的一组后继节点，每个后继节点分别对应初始数据库中的一个分量；可应用于分量数据库的每条产生式规则，也对应于一个连接符，它指向的节点则相应于应用规则后生成的数据库；满足产生式系统结束条件的数据库是对应的一组终节点；产生式系统的任务是搜索从初始节点到一组终节点集N的一个解图。