1 课前思考：
　　第二章介绍了状态空间搜索问题及有关的搜索算法。这些问题的特点是一个节点的后继节点之间是"或"的关系，只要一个节点得以求解，则该节点也就被求解了。从初始节点到目标节点之间，求解的是一条路径，也就是一个节点的序列。但在某些问题中，一个节点是否被求解，取决于该节点的部分或全部后继节点被求解，而不只是一个后继节点被求解。也就是说，对于该节点来说，其部分或全部后继节点是"与"的关系。在这种情况下，如何运用搜索技术来求解问题呢？这就是本章要讨论的可分解产生式系统的搜索问题。本章还要介绍另一类特殊的可分解产生式系统--博弈树的搜索问题。在博弈问题中--比如说象棋--搜索是在博弈者双方之间进行的，任何一方在搜索时，都必须要考虑对方可能要采用的走步，而且对于一个优秀的博弈者来说，应考虑的不只是对方一步的走法，而是若干步的走法。而且这一过程一般来说是动态进行的，也就是说，在考虑若干步走法以后，下了一步棋，而在对方走棋之后，还要再次考虑若干步走法，决定下一步的走法，而不是一劳永逸，搜索一次就决定了所有的走法。这就是本章的后半部分所要讨论的博弈树搜索问题。

2 学习目标：
　　了解一般的与或图搜索问题，掌握与或图的启发式搜索算法AO*，了解博弈树搜索问题，掌握博弈树搜索中的极小极大方法和α-β剪枝搜索方法。

3 学习指南：
　　了解算法的每一个过程和细节问题，对于给定的与或图，学会利用AO*搜索找到问题的解图。对于给定的博弈树，学会利用α-β剪枝方法搜索，得到最佳走步，在有条件的情况下，程序实现一个采用α-β剪枝算法，求解一些典型的博弈问题，如五子棋。

4 难重点：
　　AO*算法，α-β剪枝算法。

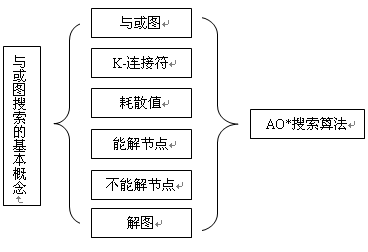
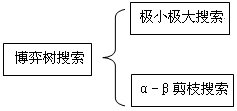
5 知识点：