3．数字魔方问题求解的搜索策略

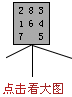
　　数字魔方游戏已有悠久的历史，是古代数学家、哲学家、神学家、占星家等探索的问题。现在来看一个1750年Benjamin Franklin编造的一个数字魔方。在8×8的棋盘方格上，填入1－64的数字，其结果如图2.19所示。

图2.19 Benjamin Franklin数字魔方

图2.20 Benjamin Franklin数字魔园

其主要特性是每行或每列8个数字的总和为260。再进一步分析发现任一半行或半列4个数字的总和为130；任一拐弯对角线8个数字的总和也是260（如16，63，57，10，23，40，34，17或50，8，7，54，43，26，25，47两条拐弯对角线）；4角的4个数字（52，45，16，17）与中心的4个数字（54，43，10，23）也是260；任意一个2×2的子魔方4个数字之和是130（如52，61，14，3或23，26，41，40），还可给出几个类似的性质。Benjamin Franklin还研究了魔圆的构造问题，9个同心圆等分为8个扇区，将12－75共64个数字填入空格中，如图2.20所示。其性质是：任一同心圆周格子上的8个数字之和加上中心圆的数字（为起始数12）总和为360；任一径向8个数字之和加上中心圆的数字总和亦为360（圆周的度数）。更为惊讶的是任一径向半列的4个相邻格子数字和加上6，其总和为180；由水平直径分割后任一半圆数字和加上6，其总和仍为180。由此看出构造这种数字魔方或魔圆并满足若干性质是一个极为复杂的搜索问题。
　　下面来讨论一个最简单的3×3数字魔方问题。将1－9共9个数码填入魔方格使行、列和对角线数码总和相等。对于奇数阶魔问题，数学家们已构造出一个极为巧妙的算法，不花费任何多余的搜索就可以直接找到问题的解。
这个算法的要点如下：
N阶（奇次）魔方算法：
① ；函数P把最小数字置于顶行中心处，每一方格用坐标标记，如图2.21。

图 2.21 魔方坐标图

②LOOP：D：＝D＋1，x：＝x＋1，y:＝y＋1；
③IF D＝N2 THEN EXIT（SUCCESS）；
④IF（x＜N）∧（y＜N）THEN IF（x，y）=NIL
THEN P(D，(x，y)）
ELSE P（D，（x－1，y-2））
IF（x＜N）∧（y＞N）THEN P（D，（x，y-N））
IF（x＞N）∧（y＜N）THEN P（D，（x-N，y））
IF（x＞N）∧（y＞N）THEN IF(x-N，y-N)=NIL
THEN P（D，（x-N，y-N））
THEN P（D，（x-1，y-2））；
⑤GO LOOP；
　　该算法应用于3×3数字魔方问题，其搜索图如图2.22所示，从搜索过程看出，构造算法的基本启发信息是把数码等分成N组，每一组N个数码放置原则是每一个数码必须处在不同行不同列的方格上，这样搭配就可能使行、列和对角线的数字和相接近乃至完全相等。这是最有希望获得目标要求的搜索方向，这样就把许多没有希望的路径删弃，从而大大提高了搜索效果。

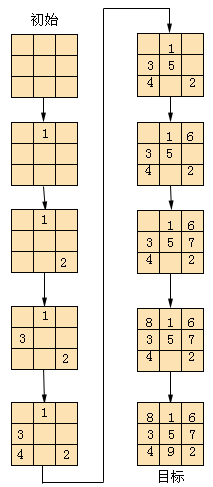
图2.22 3×3数字魔方搜索图

　　进一步分析数字魔方的要求，还可以给出若干有用的启发信息，例如N（奇次）阶魔方，行、列或对角的总和值 ，在 种的数字组合中，只有满足数字总和为S的2N＋2组排法才可能构成解。其中具有公共元的4组数字应排列在中心行、中心列和对角线上，且公共元的那个数码必定处在中心格位置上，还有3组共有的那些数码必定处在四角位置上等等。利用信息引导搜索，可求解任意阶数字魔方问题。
　　对于任意偶次阶的数字魔方问题，也有简单的求解算法，读者可从程序设计的参考书找到，这里不再介绍。