2.5 搜索算法讨论

　　1．弱方法
　　人工智能范畴的一些问题都比较复杂，一般无法用直接求解的方法找到解答，因此通常都要藉助于搜索技术。前面几节讨论的搜索方法，其描述均与问题领域无关，如果把这些方法应用于特定问题的领域时，其效率依赖于该领域知识应用的情况，从我们举过的几个例子就可说明这个问题。但由于这些方法难于克服搜索过程的组合爆炸问题，因此在人工智能领域中，把这些方法统称为"弱方法"。这些搜索方法可用来求解不存在确定求解算法的某一类问题，或者虽然有某种求解算法，但复杂性很高，有不少均属NP－完全类的问题。为避免求解过程的组合爆炸，在搜索算法中引入启发性信息，多数情况能以较少的代价找到解，但并不能保证任何情况下都能获得解，这就是所�"弱方法"的含义。当然如果引入强有力的启发信息，则求解过程就能显示出"强"的作用。下面我们来讨论用优选法求解极值这类问题时搜索过程的特点。
设状态是实数域[a，b]上实值连续函数f，求该目标函数在何处取得极值及其大小。
　　在几何学中黄金分割法的思想是在区间[0，1]间取0.618和0.382两个特殊点来考虑问题：若f(0.382)较优，则剪去[0.618，1]区段；若f(0.618)较优，则剪去[0，0.382]区段；然后在新区间依此规则继续下去，直至函数f在某一点取得极值，这就是优先法的要点。显然目标函数f中包含了启发信息，下面给出该算法（应用该算法时先把[a，b]通过变换转换成[0，1]）：
黄金分割法

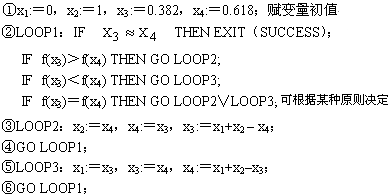
　　由于计算中引入了极强的启发信息，因而获得最佳的搜索效果，可以证明f在[0，1]间具有单极值时，f(x3)或f(x4)即为求得的极值点，而且求解过程搜索的点数是最少的。
　　前面我们讨论的几个搜索算法都属弱方法，实际上人工智能研究中提出属于这类的算法很多（如约束满足法，手段目的分析法等等），都可以用来求解某一特定问题，至于具体选择哪一种策略，很大程度上取决于问题的特征和实际要求。另外这些方法只提供了一种框架，对复杂问题只要能较好地运用特定问题的启发信息，就可能获得较好的搜索效果。