很容易证明，满足单调条件的h，一定满足A*条件，但反过来不一定成立。

　　一个启发函数h，如果对所有节点ni和nj（nj是ni的子节点），都有h(ni) - h(nj)≤C(ni，nj)或h(ni)≤C(ni，nj)＋h(nj)且h(ti)＝0，则称该h函数满足单调限制条件。其意义是从ni到目标节点，最佳路径耗散值估计h(ni)不大于nj到目标节点最佳路径耗散值估计h(nj)与ni到nj孤线耗散值两者之和。

要证明一个h是单调的，就要证明该h对于任意两个节点ni和nj（其中nj是ni的子节点），都有h(ni) - h(nj)≤C(ni，nj)，且h(ti)＝0。
当用"不在位的奖牌数"来定义八数码问题的h时（即h(n)＝W(n)），其目标的h值显然等于0。第二个条件成立。
由于八数码问题一次只能移动一个将牌，因此当移动完一个将牌后，会有以下三种情况：
（1）一个将牌从"在位"移动到了"不在位"，其结果是使得h值增加1，这时h(ni) - h(nj)＝-1；
（2）一个原来就"不在位"的将牌，移动后，还是"不在位"，其结果是使得h值不变，这时h(ni) - h(nj)＝0；
（3）一个将牌从"不在位"移动到了"在位"，其结果使得h值减少1，这时h(ni) - h(nj)＝1。
综合以上三种情况，均有h(ni) - h(nj)≤1。而由于八数码问题每走一定耗散值为1，所以有C(ni，nj)＝1。所以有：h(ni) - h(nj)≤C(ni，nj)，单调条件的第一条也被满足。所以当用"不在位的奖牌数"来定义八数码问题的h时，该h是单调的。

对八数码问题，h(n)＝W(n)是满足单调限制的条件。

定理5：若h(n)满足单调限制条件，则A*扩展了节点n之后，就已经找到了到达节点n的最佳路径。即若A*选n来扩展，在单调限制条件下有g(n)=g*(n)。

　　如果先证明定理6，反过来再证明定理5，定理5的证明将会简单一些。由定理6我们知道，当h满足单调条件时，A*所扩展的节点序列其f值是非递减的。也就是说，后扩展的节点的f值，不会比先扩展的节点的f值小。设从初始节点s到节点n有两条路径存在。第一次扩展n时得到的路径设为p1，其耗散值为f1(n)=g1(n)+h(n)。第二次扩展n时得到的路径设为p2，其耗散值为f2(n)=g2(n)+h(n)。根据定理6，有f2(n)≥f1(n)，所以有g2(n)≥g1(n)，所以第一次扩展n时，就得到了从初始路径s到n的最优路径。

证明：设n是A*选作扩展的任一节点，若n＝s，显然有g(s)＝g*(s)＝0，因此考虑n≠s的情况。
我们用序列P＝（n0＝s，n1，…，nk＝n）表达到达n的最佳路径。现在从OPEN中取出非初始节点n扩展时，假定没有找到P，这时CLOSED中一定会有P中的节点（至少s是在CLOSED中，n刚被选作扩展，不在CLOSED中），把P序列中（依顺序检查）最后一个出现在CLOSED中的节点称为nj，那么nj+1是在OPEN中（nj+1≠n），由单调限制条件，对任意i有
g*(ni) + h(ni)≤g*(ni) + C(ni，ni+1) + h(ni+1) （1）
因为ni和ni+1在最佳路径上，所以有
g*(ni+1)＝g*(ni) + C(ni ，ni+1)
代入（1）式后有g*(ni) + h(ni)≤g*(ni+1) + h(ni+1)
这个不等式对P上所有相邻的节点都合适，若从i＝j到i＝k-1应用该不等式，并利用传递性有
g*(nl+1)+h(nl+1)≤g*(nk)+h(nk)
即 f(nl+1)≤g*(n)+h(n) （2）
另一方面，A*选n来扩展，必有
f(n)＝g(n)+h(n)≤f(nj+1) （3）
比较（2）、（3）得g(n)≤g*(n)，但已知g(n)≥g*(n)，因此选n扩展时必有g(n)＝g*(n)，即找到了到达n的最佳路径。
[证毕]

定理6：若h(n)满足单调限制，则由A*所扩展的节点序列，其f值是非递减的，即f(ni)≤f(nj)
证明：由单调限制条件：
h(ni) - h(nj)≤C(ni，nj)
即 f(ni) - g(ni) - f(nj) + g(nj)≤C(ni，nj)
f(ni) - g(ni) - f(nj) + g(ni)＋C(ni，nj)≤C(ni，nj)
f(ni) - f(nj)≤0。[证毕]

前面分析过，之所以会出现重复节点扩展问题，就是因为A*在扩展n时，并不能保证找到从s到n的最优路径，从而出现重复节点扩展问题。而定理5则保证了当h满足单调条件时，第一次扩展n时，就已经找到了到达n的最佳路径。从而如果h满足单调条件，就一定不会出现重复扩展节点问题。

根据定理5，在应用A*算法时，在第6步可不必进行节点的指针修正操作，因而改善了A*的效率。

另一方面我们从图2.12的例子看出，因h不满足单调限制条件，在扩展节点n时，有可能还没有找到到达n的最佳路径，因此该节点还会再次被放入OPEN中，从而造成了该节点被重复扩展。
为了使A*算法少进行重复扩展，对A算法做如下的修改，称为修正过程A（修正的A算法）。

　　定义满足单调条件的h，是避免重复扩展节点的好办法。但是对于实际问题来说，定义一个单调的h并不是一件很容易的事，那么能否通过修改算法，来达到避免或者减少重复节点扩展的问题呢？答案是肯定的。只要适当地修改A算法，就可以达到这样的目的。
　　我们说过，在改进A*算法的时候，一是要保持A*算法的可采纳性，二是不能增加过多的计算工作量。由推论2.1我们知道，OPEN表上任一具有f(n) < f*(s)的节点n定会被扩展。由推论3.1我们知道，A*选作扩展的任一节点，定有f(n)≤f*(s)。这两个推论正是我们改进A*算法的理论基础。
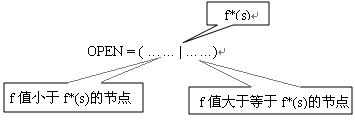
算法改进的基本思路是：如下图所示，我们仍像A*算法那样，按照节点的f值从小到大排序OPEN表中的节点，我们以f*(s)为界将OPEN表划分为两部分，一部分由那些f值小于f*(s)的节点组成，我们称其为NEST，其他的节点属于另一个部分。