7．A*算法的改进

　　在A算法的第六步，对于ml类节点，存在重新放回到OPEN表的可能，因此一个节点有可能被反复扩展多次。因此单纯用"扩展的节点数"并不能客观地来评判搜索算法的好坏。因为即便是扩展的节点数比较少，但如果很多节点被多次重复扩展的话，搜索效率同样是很低的。

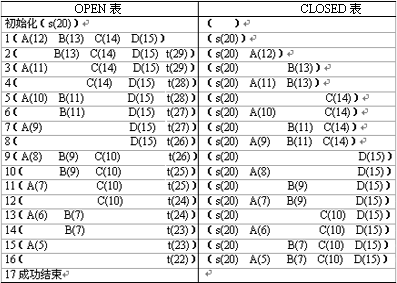
　　上一节讨论了启发函数对扩展节点数所起的作用。如果用扩展节点数作为评价搜索效率的准则，那么可以发现A算法第6步中，对m1类节点要重新放回OPEN表中的操作，将引起多次扩展同一个节点的可能，因而即使扩展的节点数少，但重复扩展某些节点，也将导致搜索效率下降。图2.12给出同一节点多次扩展的例子，并列出了调用算法A*过程时OPEN和CLOSED表的状态。从CLOSED表可以看出，在修改m1类节点指针过程中，节点A、B、C重复扩展，次数分别为8、4、2，总共扩展16次节点。

　　通过这个例子使我们看到确实有重复扩展节点的想象存在。为什么会有重复扩展一个节点的现象发生呢？主要就是因为在扩展一个节点时，A*并不能保证此时就已经找到了从初始节点s到当前节点n的最短路径，使得算法在第六步，有可能将其重新放回到OPEN表中，而放入OPEN表以后，该节点就有可能被再次扩展。
　　有没有办法避免或者减少重复扩展节点的情况发生呢？答案是肯定的。主要途径有两个，一个是对启发函数h进一步加上限制，使得A*算法在扩展一个节点n时，就已经找到了从初始节点s到当前节点n的最短路径，这样就避免了将n重新放回到OPEN表中的可能，从而避免了重复扩展节点现象的发生。另一个是还是使用原来的A*对启发函数h的限制条件，但改变算法本身，使之减少重复扩展节点现象。但这种对算法的改变要坚持两点，一是要保持A*算法的可采纳性，不能因为减少了重复扩展节点，而失去可采纳性；二是不能增加过多的计算工作量，不然重复扩展节点问题解决了，但增加了计算工作量，没有达到提高搜索效率的目的。
　　从这个例子看出，如果不使用启发函数，则每个节点仅扩展一次，虽然扩展的节点数相同，但A*扩展的次数多。如果对启发函数施加一定的限制--单调限制，则当A*算法选某一个节点扩展时，就已经找到到该节点的最佳路径。下面就来证明这个结论。

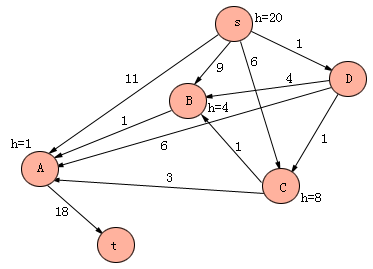
图2.12 A*算法多次扩展同一节点搜索图例子

注意，h是单调的条件中，必须包含h(ti)＝0这个条件，其中ti是目标节点之一。