6．启发函数与A*算法的关系

应用A*的过程中，如果选作扩展的节点n，其评价函数值f(n)=f*(n)，则不会去扩展多余的节点就可找到解。可以想象到f(n)越接近于f*(n)，扩展的节点数就会越少，即启发函数中，应用的启发信息（问题知识）愈多，扩展的节点数就越少。

在定理4中所说的"有两个A*算法A1和A2"，指的是对于同一个问题，分别定义了两个启发函数h1和h2。这里要强调几点：首先，这里的A1和A2都是A*的，也就是说定义的h1和h2都要满足A*算法的条件。第二，只有当对于任何一个节点n，都有h2(n)>h1(n)时，定理才能保证用A2搜索所扩展的节点数≤用A1搜索所扩展的节点数。而如果仅是h2(n)≥h1(n)时（比定理的条件多了一个"等于"，而不只是单纯的"大于"），定理并不能保证用A2搜索所扩展的节点数≤用A1搜索所扩展的节点数。也就是说，如果仅是h2(n)≥h1(n)，有等于的情况出现，可能会有用A2搜索所扩展的节点数反而多于用A1搜索所扩展的节点数的情况。这种情况一般只会在有多个节点的f值相等时，才可能出现，这是由于A算法对于具有相等的f值的节点，并没有规定其扩展次序造成的。一般来说，对于大多数实际问题，即便是h2(n)≥h1(n)时，用A2搜索所扩展的节点数也不会比用A1搜索所扩展的节点数多。第三，这里所说的"扩展的节点数"，是这样来计算的，同一个节点不管它被扩展多少次（在A算法的第六步，对于ml类节点，存在重新放回到OPEN表的可能，因此一个节点有可能被反复扩展多次，在后面我们会看到这样的例子），在计算"扩展的节点数"时，都只计算一次，而不管它被重复扩展了多少次。
该定理的意义在于，在使用A*算法求解问题时，定义的启发函数h，在满足A*的条件下，应尽可能地大一些，使其接近于h*，这样才能使得搜索的效率高。

定理4：有两个A*算法A1和A2，若A2比A1有较多的启发信息（即对所有非目标节点均有h2(n)>h1(n)），则在具有一条从s到t的隐含图上，搜索结束时，由A2所扩展的每一个节点，也必定由A1所扩展，即A1扩展的节点至少和A2一样多。
证明：使用数学归纳法，对节点的深度应用归纳法。
（1）对深度d(n)=0的节点（即初始节点s），定理结论成立，即若s为目标节点，则A1和A2都不扩展s，否则A1和A2都扩展了s（归纳法前提）。
（2）设深度d(n)≤=k，对所有路径的端节点，定理结论都成立（归纳法假设）。
（3）要证明d(n)＝k+1时，所有路径的端节点，结论成立，我们用反证法证明。
设A2搜索树上有一个节点n（d(n)=k+1）被A2扩展了，而对应于A1搜索树上的这个节点n，没有被A1扩展。根据归纳法假设条件，A1扩展了n的父节点，n是在A1搜索树上，因此A1结束时，n必定保留在其OPEN表上，n没有被A1选择扩展，有
f1(n)≥f*(s)，即g1(n)+h1(n)≥f*(s)
所以 h1(n)≥f*(s) - g1(n) （1）
另一方面A2扩展了n，有
f2(n)≤f*(s)，即g2(n)+h2(n)≤f*(s)
所以 h2(n)≤f*(s)-g2(n) （2）
由于d=k时，A2扩展的节点，A1也一定扩展，故有
g1(n)≤g2(n)（因A1扩展的节点数可能较多）
所以 h1(n)≥f*(s) - g1(n)≥f*(s) - g2(n) （3）
比较式（2）、（3）可得：至少在节点n上有h1(n)≥h2(n)，这与定理的前提条件矛盾，因此存在节点n的假设不成立。[证毕]

由这个定理可知，使用启发函数h(n)的A*算法，比不使用h(n) (h(n)≡0)的算法，求得最佳路径时扩展的节点数要少，图2.11的搜索图例子可看出比较的结果。当h≡0时，求得最佳解路（s，C，J，t7），其f*(s)=8，但除t1~t8外所有节点都扩展了，即求出所有解路后，才找到耗散值最小的路径。而引入启发函数（设其函数值如图中节点旁边所示）后，除了最佳路径上的节点s，C，J被扩展外，其余的节点都没有被扩展。当然一般情况下，并不一定都能达到这种效果，主要在于获取完备的启发信息较为困难。

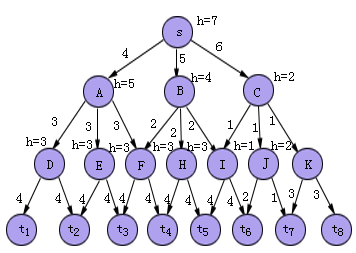
图2.11启发函数h(n)的效果比较