4．动态规划法

在A算法中，当h(n)≡0时，则A算法演变为动态规划算法。由于在A算法中，很多问题的启发函数h难于定义，因此动态规划算法是至今一直被经常使用的算法。在其他方面的一些书中--如运筹学方面的书--讲到的动态规划方法，在形式上可能与这里介绍的有所不同，但其性质是一样的，而且这里所介绍的动态规划方法，具有更多的灵活性。

动态规划法实际上是对分支界限法的改进。从图2.9看出，第二循环扩展A（3）后生成的D（8）节点（D（4）已在QUEUE上）和第三循环扩展D（4）之后生成的A（9）节点（A（3）已以QUEUE上）都是多余的分支，因为由s－D到达目标的路径显然要比s－A－D到达目标的路径要好。因此删去类似于s－A－D或s－D－A这样一些多余的路径将会大大提高搜索效率。动态规划原理指出，求s→t的最佳路径时，对某一个中间节点I，只要考虑s到I中最小耗散值这一条局部路径就可以，其余s到I的路径是多余的，不必加以考虑。下面给出具有动态规划原理的分支界限算法。
过程Dynamic-Programming
①QUEUE:=(s-s)，g(s)=0;
②LOOP：IF QUEUE=（ ） THEN EXIT(FAIL);
③PATH:=FIRST(QUEUE)，n:=LAST(PATH);
④IF GOAL(n) THEN EXIT(SUCCESS);
⑤EXPAND(n)→{mi}，计算g(mi)=g(n，mi)，REMOVE（s-n，QUEUE），ADD(s-mi，QUEUE);
⑥若QUEUE中有多条到达某一公共节点的路径，则只保留耗散值最小的那条路径，其余删去，并重新排序，g值最小者排在前面；
⑦GO LOOP；
对图2.8的例子应用该算法，其搜索图如图2.10所示，实际只剩下两条搜索路径，改善了搜索效率。

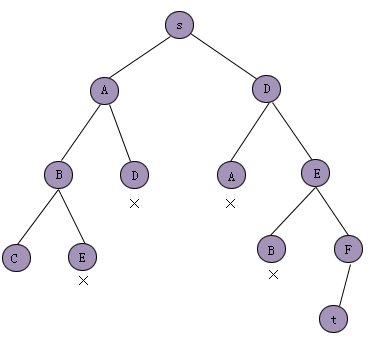
图2.10 动态规划原理的搜索树