2．爬山法

过程Hill-climbing
①n:=s；s为初始节点
②LOOP：IF GOAL（n）THEN EXIT (SUCCESS)；
③EXPAND（n）→{mi}，计算h(mi)，nextn:=m(min h(mi)的节点)；
④IF h(n)<h(nextn) THEN EXIT(FAIL);
⑤n:=nextn；
⑥GO LOOP；
显然如果将山顶作为目标，h(n)表示山顶与当前位置n之间高度之差，则该算法相当于总是登向山顶，在单峰的条件下，必能到达山峰。

3．分支界限法

分支界限法是优先扩展当前具有最小耗散值分支路径的端节点n，其评价函数为f(n)=g(n)。该算法的基本思想很简单，实际上是建立一个局部路径（或分支）的队列表，每次都选耗散值最小的那个分支上的端节点来扩展，直到生成出含有目标节点的路径为止。
过程Branch-Bound
①QUEUE:=(s-s)，g(s)=0;
②LOOP：IF QUEUE=( ) THEN EXIT(FAIL);
③PATH:=FIRST(QUEUE)，n:=LAST(PATH);
④IF GOAL(n) THEN EXIT(SUCCESS);
⑤EXPAND(n)→{mi}，计算g(mi)=g(n，mi)，REMOVE（s - n，QUEUE），ADD(s-mi，QUEUE);
⑥QUEUE中局部路径g值最小者排在前面；
⑦GO LOOP；

应用该算法求解图2.8的最短路径问题，其搜索图如图2.9所示，求解过程中QUEUE的结果简记如下（D(4)代表耗散值为4的s-D分支，其余类推）：

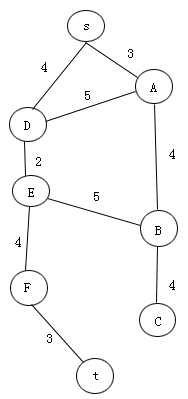
图2.8 八城市地图示意图

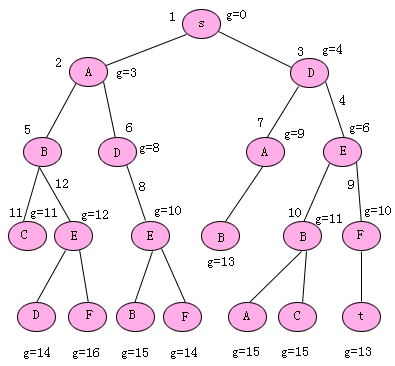
图2.9 分支界限搜索树

初始（s(0)）
1.（A（3）D（4））
2.（D（4）B（7）D（8））
3.（E（6）B（7）D（8）A（9））
4.（B（7）D（8）A（9）F（10）B（11））
5.（D（8）A（9）F（10）B（11）C（11）E（12））
6.（A（9）E（10）F（10）B（11）C（11）E（12））
7.（E（10）F（10）B（11）C（11）E（12）B（13））
8.（F（10）B（11）C（11）E（12）B（13）F（14）B（15））
9.（B（11）C（11）E（12）t（13）B（13）F（14）B（15））
10.（C（11）E（12）t（13）B（13）F（14）A（15）B（15）C（15））
11.（E（12）t（13）B（13）F（14）A（15）B（15）C（15））
12.（t（13）B（13）F（14）D（14）A（15）B（15）C（15）F（16））
13.结束。