1.启发式搜索算法A
启发式搜索算法A,一般简称为A算法,是一种典型的启发式搜索算法。其基本思想是:定义一个评价函数f,对当前的搜索状态进行评估,找出一个最有希望的节点来扩展。
评价函数的形式如下:
f(n)=g(n)+h(n)
其中n是被评价的节点。
f(n)、g(n)和h(n)各自表述什么含义呢?我们先来定义下面几个函数的含义,它们与f(n)、g(n)和h(n)的差别是都带有一个"*"号。
g*(n):表示从初始节点s到节点n的最短路径的耗散值;
h*(n):表示从节点n到目标节点g的最短路径的耗散值;
f*(n)=g*(n)+h*(n):表示从初始节点s经过节点n到目标节点g的最短路径的耗散值。
而f(n)、g(n)和h(n)则分别表示是对f*(n)、g*(n)和h*(n)三个函数值的的估计值。是一种预测。A算法就是利用这种预测,来达到有效搜索的目的的。它每次按照f(n)值的大小对OPEN表中的元素进行排序,f值小的节点放在前面,而f值大的节点则被放在OPEN表的后面,这样每次扩展节点时,都是选择当前f值最小的节点来优先扩展。
利用评价函数f(n)=g(n)+h(n)来排列OPEN表节点顺序的图搜索算法称为算法A。
过程A
①OPEN:=(s),f(s):=g(s)+h(s);
②LOOP:IF OPEN=( )THEN EXIT(FAIL);
③n:=FIRST(OPEN);
④IF GOAL(n)THEN EXIT(SUCCESS);
⑤REMOVE(n,OPEN),ADD(n,CLOSED);
⑥EXPAND(n)→{mi},计算f(n,mi)=g(n,mi)+h(mi);g(n,mi)是从s通过n到mi的耗散值,f(n,mi)是从s通过n、mi到目标节点耗散值的估计。
・ADD(mj,OPEN),标记mi到n的指针。
・IF f(n,mk)<f(mk)THEN f(mk):=f(n,mk),标记mk到n的指针;比较f(n,mk)和f(mk),f(mk)是扩展n之前计算的耗散值。
・IF f(n,m1)<f(m1)THEN f(m1):=f(n,m1),标记m1到n的指针,ADD(m1,OPEN);当f(n,m1)<f(m1)时,把m1重放回OPEN中,不必考虑修改到其子节点的指针。
⑦OPEN中的节点按f值从小到大排序;
⑧GO LOOP;
A算法同样由一般的图搜索算法改变而成。在算法的第7步,按照f值从小到大对OPEN表中的节点进行排序,体现了A算法的含义。
算法要计算f(n)、g(n)和h(n)的值,g(n)根据已经搜索的结果,按照从初始节点s到节点n的路径,计算这条路径的耗散值就可以了。而h(n)是与问题有关的,需要根据具体的问题来定义。有了g(n)和h(n)的值,将他们加起来就得到f(n)的值了。
在介绍一般的图搜索算法时我们就曾经让大家注意过,在这里我们再强调一次,请大家注意A算法的结束条件:当从OPEN中取出第一节点时,如果该节点是目标节点,则算法成功结束。而不是在扩展一个节点时,只要目标节点一出现就立即结束。我们在后面将会看到,正是由于有了这样的结束判断条件,才使得A算法有很好的性质。
算法中f(n)规定为对从初始节点s出发,约束通过节点n到达目标点t,最小耗散值路径的耗散值f*(n)的估计值,通常取正值。f(n)由两个分量组成,其中g(n)是到目前为止,从s到n的一条最小耗散值路径的耗散值,是作为从s到n最小耗散值路径的耗散值g*(n)的估计值,h(n)是从n到目标节点t,最小耗散值路径的耗散值h*(n)的估计值。
设函数k(ni,nj)表示最小耗散路径的实际耗散值(当ni到nj无通路时则k(ni,nj)无意义),则g*(n)=k(s,n),h*(n)=min
k(n,ti),其中ti是目标节点集,k(n,ti)就是从n到每一个目标节点最小耗散值路径的耗散值,h*(n)是其中最小值的那条路径的耗散值,而具有h*(n)值的路径是n到ti的最佳路径。由此可得f*(n)=g*(n)+h*(n)就表示s→ti并约束通过节点n的最佳路径的耗散值。当n=s时,f*(s)=h*(s)则表示s→ti无约束的最佳路径的耗散值,这样一来,所定义的f(n)=g(n)+h(n)就是对f*(n)的一个估计。g(n)的值实际上很容易从到目前为止的搜索树上计算出来,不必专门定义计算公式,也就是根据搜索历史情况对g*(n)作出估计,显然有g(n)≥g*(n)。 h(n)则依赖于启发信息,通常称为启发函数,是要对未来扩展的方向作出估计。算法A是按f(n)递增的顺序来排列OPEN表的节点,因而优先扩展f(n)值小的节点,体现了好的优先搜索思想,所以算法A是一个好的优先的搜索策略。图2.6表示出当前要扩展节点n之前的搜索图,扩展n后新生成的子节点m1(∈{mj})、m2(∈{mk})、m3(∈{m1})要分别计算其评价函数值:
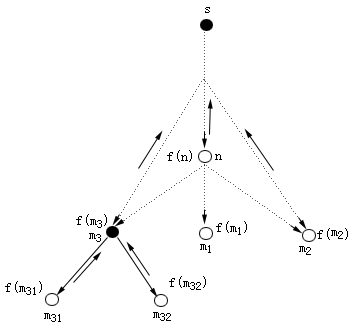
图2.6 搜索示意图
f(m1)=g(m1)+h(m1)
f(n,m2)=g(n,m2)+h(m2)
f(n,m3)=g(n,m3)+h(m3)
然后按第6步条件进行指针设置和第7步重排OPEN表节点顺序,以便确定下一次要扩展的节点。
用A算法来求解一个问题,最主要的就是要定义启发函数h(n)。对于8数码问题,一种简单的启发函数的定义是:
h(n) = 不在位的将牌数
什么是"不在位的将牌数"呢?我们来看下面的两个图。

其中左边的图是8数码问题的一个初始状态,右边的图是8数码问题的目标状态。我们拿初始状态和目标状态相比较,看初始状态的哪些将牌不在目标状态的位置上,这些将牌的数目之和,就是"不在位的将牌数"。比较上面两个图,发现1、2、6和8四个将牌不在目标状态的位置上,所以初始状态的"不在位的将牌数"就是4,也就是初始状态的h值。其他状态的h值,也按照此方法计算。
下面再以八数码问题为例说明好的优先搜索策略的应用过程。设评价函数f(n)形式如下:
f(n)=d(n)+W(n)
其中d(n)代表节点的深度,取g(n)=d(n)表示讨论单位耗散的情况;取h(n)=W(n)表示"不在位"的将牌个数作为启发函数的度量,这时f(n)可估计出通向目标节点的希望程度。图2.7表示使用这种评价函数时的搜索树,图中括弧中的数字表示该节点的评价函数值f。算法每一循环结束时,其OPEN表和CLOSED表的排列如下:

根据目标节点L返回到s的指针,可得解路径S(4),B(5),E(5),I(5),K(5),L(5)
图2.7给出的是使用A算法求解8数码问题的搜索图。其中A、B、C等符号,只是为了标记节点的名称,没有特殊意义。这些符号旁边括弧中的数字是该节点的评价函数值f。而圆圈中的值,则表示节点的扩展顺序。
从图中可以看出,在第二步选择节点B扩展之后,OPEN表中f值最小的节点有D和E两个节点,他们的f值都是5。在出现相同的f值时,A算法并没有规定首先扩展哪个节点,可以任意选择其中的一个节点首先扩展。
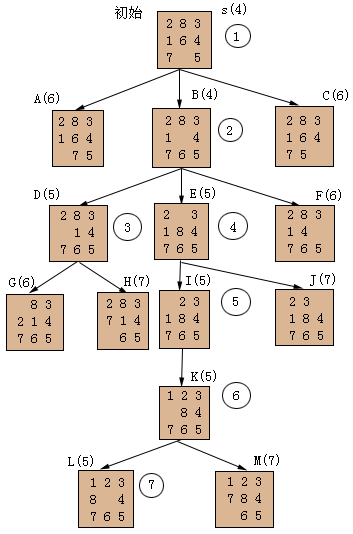
图2.7 八数码问题的搜索树