9．评价函数的启发能力

　　首先我们通过八数码问题为例说明A算法的启发能力与选择启发函数h(n)的关系。一般来说启发能力强，则搜索效率较高。有时选用不是h*(n)下界范围的h(n)时，虽然会牺牲找到最佳解的性能，但可使启发能力得到改善，从而有利于求解一些较难的问题。
　　求解这个八数码问题，使用启发函数h(n)＝P(n)时，仍不能估计出交换相邻两个将牌位置难易程序的影响，为此可再引入S(n)分量。S(n)是对节点n中将牌排列顺序的计分值，规定对非中心位置的将牌，顺某一方向检查，若某一将牌后面跟的后继者和目标状态相应将牌的顺序相比不一致时，则该将牌估分取2，一致时则估分取0；对中心位置有将牌时估分取1，无将牌时估分值取0；所有非中心位置每个将牌估分总和加上中心位置的估分值定义为S(n)。依据这些启发信息，取h(n)＝P(n)+3S(n)时，就是用f(n)＝g(n)+P(n)+3S(n)来估计最佳路径的耗散值。f(n)值小的节点，确能反映该节点愈有希望处于到达目标节点的最佳路径上。图2.18给出了该问题的搜索树，图中给出各节点的f值，圆圈中的数字表示扩展顺序。由图看出h(n)函数不满足下界范围，但在该问题中，刚好找到了最小长度（18步）的解路径。

　　该例子给了一个不满足A*条件的h函数。从图上可以看出，启发效果非常的好，对于需要18步才能完成的8数码问题，几乎没有扩展什么多余的节点，就找到了解路径。这里所用的方法一是组合两个不同的启发函数；二是采取加权的方法（这里对S(n)加权为3），来加大S(n)的作用。这样得到的启发函数由于不满足A*条件，因此不能保证找到问题的最佳解，但往往可以提高搜索效率，加快找到解的速度。由于这样的启发函数还是反映了被评估节点到目标节点路径耗散值的多少，算法虽然不能一定找到最优解，但一般来说，找到的也是一个可以被接受的满意解。很多情况下，满意解就足够了，最优解并没有什么特殊的意义，二者可能相差很少，但却使得问题简单了很多。值得指出的是，该例子所得到的解，刚好是一个最优解。
　　还有一个决定搜索算法启发能力的因素是涉及到计算启发函数的工作量，从被扩展的节点数最少的角度看，h≡h*最优，但这可能导致繁重的计算工作量。有时候一个不是h*下界范围的h函数可能比起下界范围的h函数更容易计算，而且被扩展节点的总数可以减少，使启发能力加倍得到改善，虽然牺牲了可采纳性，但从启发能力的角度看仍是可取的。

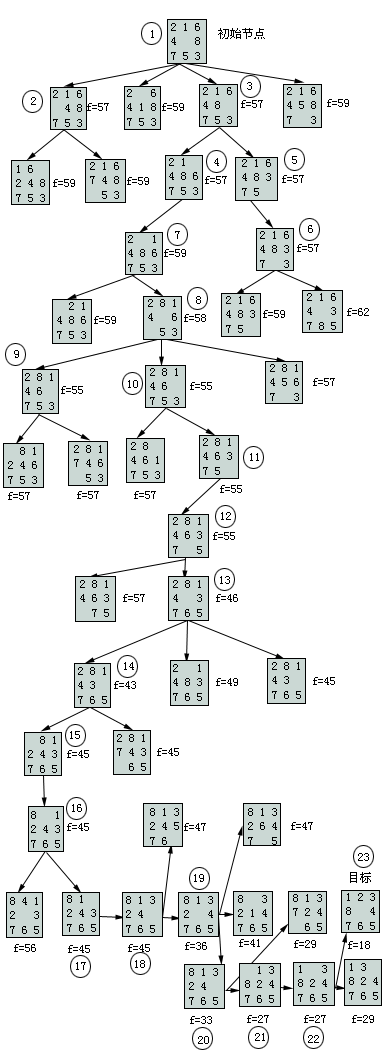
图2.18 h(n)＝P(n)+3S(n)的搜索树

　　在某些情况下，要改变启发能力，可以通过对h函数乘以加权系数的简单方法实现。当加权系数很大时，g分量的作用相对减弱，因而可略去不计，这相当于在搜索期间任何阶段上，我们不在乎到目前为止所得到的路径耗散值，而只关心找到目标节点所需的剩余工作量，即可以使用f≡h作为评价函数来对OPEN表上的节点排序。但是另一方面为了保证最终能找到通向目标节点的路径，即便并不要求寻找一条最小耗散的路径，也还是应当考虑g的作用。特别是当h不是一个理想的估计时，在f中把g考虑进去就是在搜索中添加一个宽度优先分量，从而保证了隐含图中不会有某些部分不被搜索到。而只扩展h值最小的节点，则会引起搜索过程扩展了一些靠不住的节点。
　　评价函数中，g和h相对比例可通过选择f＝g+wh中w的大小加以控制。w是一个正数，很大的w值则会过份强调启发分量，而过小的w值则突出宽度优先的特征。经验证明使w值随搜索树中节点深度成反比变化，可提高搜索效率。即在深度浅的地方，搜索主要依赖于启发分量；而较深的地方，搜索逐渐变成宽度优先，以保证到达目标的某一条路径最终被找到。
总结以上讨论，得出影响算法A启发能力的三个重要因素是：
（1）路径的耗散值；
（2）求解路径时所扩展的节点数；
（3）计算h所需的工作量。
因此选择h函数时，应综合考虑这些因素以便使启发能力最大。