(3)迷宫问题
迷宫图从入口到出口有若干条通路,求从入口到出口处最短路径的走法。 图2.15为一简单迷宫示意图及其平面坐标表示。以平面坐标图来表示迷宫的通路时,问题的状态以所处的坐标位置来表示,即综合数据库定义为(x,y),1≤x,y≤N,则迷宫问题归结为求(1,1)――>(4,4)的最短路径问题。
图2.15迷宫问题及其表示
迷宫走法规定为向东、南、西、北前进一步,由此可得规则集简化形式如下:
R1:if (x,y) then (x+1,y)
R2:if (x,y) then (x,y-1)
R3:if (x,y) then (x-1,y)
R4:if (x,y) then (x,y+1)
对于这个简单例子,可给出状态空间如图2.16所示。
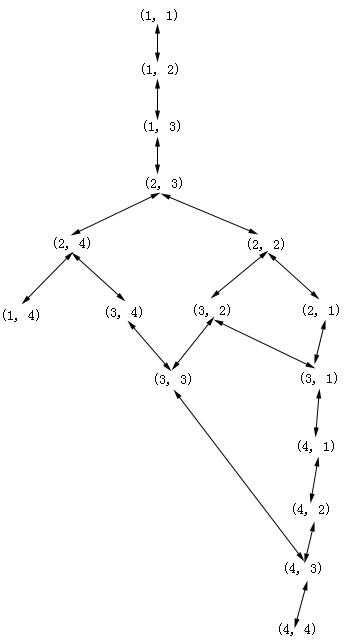
图2.16状态空间图
为求得最佳路径,可使用A*算法。假定搜索一步取单位耗散,则可定义:
由于该迷宫问题所有路都是水平或垂直的,没有斜路,因此,h(n)=|XG - Xn| + |YG - yn|显然可以满足A*的条件。
h(n)=|XG - xn| + |YG - yn|
其中(XG,YG)为目标点坐标,(xn,yn)为节点n的坐标,显然有h(n)≤h*(n)。取g(n)=d(n),有f(n)=d(n)+h(n)。再设当不同节点的f值相等时,以深度优先排序,则搜索图如图2.17所示。最短路径为((1,1),(2,3),(2,4),(3,4),(3,3),(4,3),(4,4))。
在该搜索图中,目标节点的f是8,有几个节点的f值也是8,那么这几个f值为8的节点,也有被扩展的可能,就看他们在OPEN表中的具体排列次序了。这里假定了f值相等时,以深度优先排序。
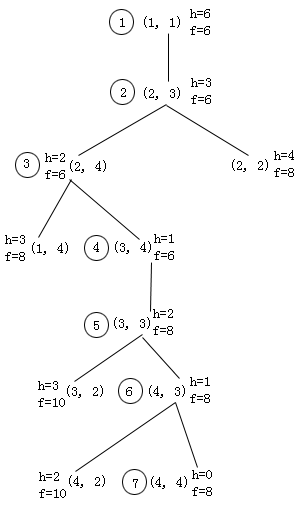
图2.17 迷宫问题启发式搜索图