（2）M-C问题

　　要说明h(n)＝M+C不满足A*条件是很容易的，只需要给出一个反例就可以了。比如状态(1, 1, 1)，h(n)=M+C=1+1=2，而实际上只要一次摆渡就可以达到目标状态，其最优路径的耗散值为1。所以不满足A*的条件。
　　下面我们来证明h(n)＝M+C-2B是满足A*条件的。
　　我们分两种情况考虑。先考虑船在左岸的情况。如果不考虑限制条件，也就是说，船一次可以将三人从左岸运到右岸，然后再有一个人将船送回来。这样，船一个来回可以运过河2人，而船仍然在左岸。而最后剩下的三个人，则可以一次将他们全部从左岸运到右岸。所以，在不考虑限制条件的情况下，也至少需要摆渡 次。其中分子上的"－3"表示剩下三个留待最后一次运过去。除以"2"是因为一个来回可以运过去2人，需要 个来回，而"来回"数不能是小数，需要向上取整，这个用符号 表示。而乘以"2"是因为一个来回相当于两次摆渡，所以要乘以2。而最后的"＋1"，则表示将剩下的3个运过去，需要一次摆渡。
化简有：


　　再考虑船在右岸的情况。同样不考虑限制条件。船在右岸，需要一个人将船运到左岸。因此对于状态(M，C，0)来说，其所需要的最少摆渡数，相当于船在左岸时状态(M+1，C，1)或(M，C+1，1)所需要的最少摆渡数，再加上第一次将船从右岸送到左岸的一次摆渡数。因此所需要的最少摆渡数为：(M+C+1)-2+1。其中(M+C+1)的"＋1"表示送船回到左岸的那个人，而最后边的"＋1"，表示送船到左岸时的一次摆渡。
化简有：(M+C+1)-2+1=M+C。
　　综合船在左岸和船在右岸两种情况下，所需要的最少摆渡次数用一个式子表示为：M+C-2B。其中B＝1表示船在左岸，B＝0表示船在右岸。
　　由于该摆渡次数是在不考虑限制条件下，推出的最少所需要的摆渡次数。因此，当有限制条件时，最优的摆渡次数只能大于等于该摆渡次数。所以该启发函数h是满足A*条件的。

设M＝C＝5，K≤3，由分析可知至少要往返10次才可能把全部M和C摆渡到右岸，因此M和C的线性组合可作为启发函数的基本分量，此外还可以考虑有船与否对摆渡的影响。图2.14给出h(n)＝0、h(n) =M+C、h(n)＝M+C-2B三种启发函数的搜索图（假定为单位耗散）。可以看出h(n)＝0的搜索图就是该问题的状态空间图；取h(n)＝M+C不满足h(n)≤h*(n)条件；只有h(n)＝M+C-2B可满足h(n)≤h*(n)。
在图2.14所示的几个搜索图中，圆圈中的数字表示节点扩展的顺序。当出现f值相同的节点时，其扩展顺序是任意的，所以节点的扩展的顺序并不是唯一的。

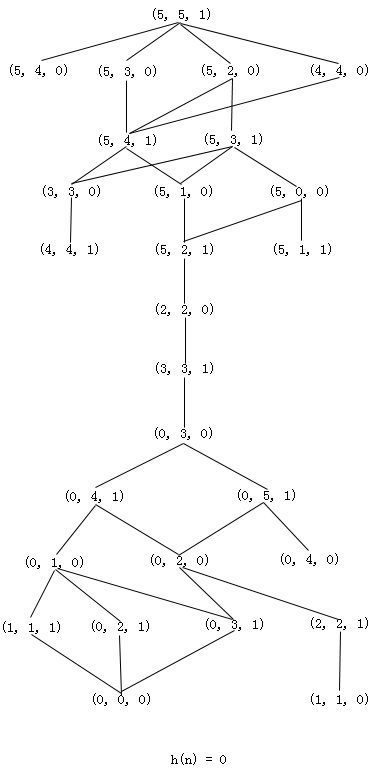
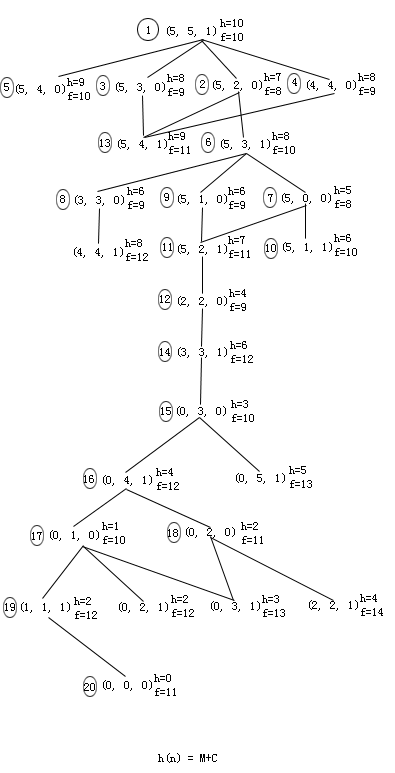
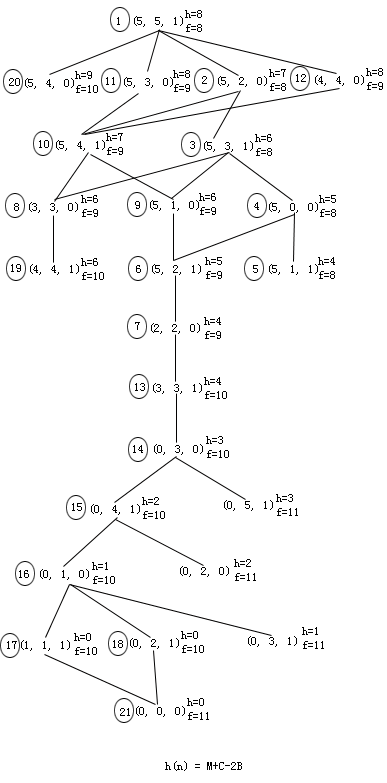
图2.14 M－C问题搜索图