8．A*算法应用举例

　　算法的理论意义在于给出了求解最佳解的条件h(n)≤h*(n)。对给定的问题，函数h*(n)（n是变量）在问题有解的条件下客观上是存在的，但在问题求解过程中不可能明确知道，因此对实际问题，能不能使所定义的启发函数满足下界范围条件？如果困难很大，那么算法的实际应用就会受到限制。下面将通过几个应用实例来说明这个问题。

　　（1）八数码问题

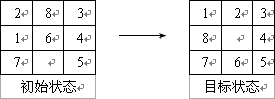
　　很容易证明h(n)=P(n)是满足A*条件的。假设某将牌距离目标位置的距离是m，即便不考虑将牌当前的位置到达目标位置之间存在其他将牌的情况，也至少要移动m步才能移到目标位置，所以对于该将牌来说，到达目标位置的耗散值至少为m。由于一个将牌的移动都是单步进行的，没有交换将牌等这样的操作。所以要把所有的不在位的将牌，移动到各自的目标位置上，至少要移动从他们各自的位置到目标位置的距离和这么多次，所以最优路径的耗散值不会比该值小，因此该启发函数h满足A*的条件。
　　另外，也可以象前面我们证明"不在位"的将牌数满足单调条件一样的方法来证明h(n)=P(n)是满足单调条件的，而满足单调条件的h(n)一定满足A*条件。

　　对八数码问题，如果启发函数根据任意节点与目标之间的差异来定义，例如取h(n)＝W(n)，那么很容易看出，尽管我们对具体的h*(n)是多少很难确切知道，但根据"不在位"将牌个数这个估计，就能得出至少要移动W(n)步才能达到目标，显然有W(n)≤h*(n)（假定为单位耗散的情况）。如果启发函数进一步考虑任意节点与目标之间距离的信息，例如取h(n)＝P(n)，P(n)定义为每一个将牌与其目标位置之间距离（不考虑夹在其间的将牌）的总和，那么同样能断定至少也要移动P(n)步才能达到目标，因此有P(n)≤h*(n)。图2.13给出h(n)＝P(n)时的搜索图，节点旁边还标出W(n)和P(n)启发函数值。由解路可给出g*(n)和h*(n)的值，由此可得最佳路径上的节点有f*＝g*+h*＝5。

　　下面给出该八数码问题取不同启发函数，应用A*算法求得最佳解时所扩展和生成的节点数。

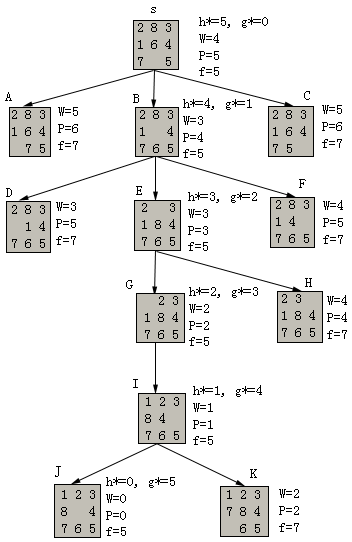
图2.13 h(n)=P(n)的搜索树