2.3 无信息图搜索过程

　　无信息图搜索属于盲目搜索，这里给两种常用的无信息图搜索方法：深度优先搜索和宽度优先搜索。

　　无信息图搜索过程是在算法的第8步中使用任意排列OPEN表节点的顺序，通常有两种排列方式：

　　该算法是根据一般的图搜索算法改变而成的。所谓深度优先搜索，就是在每次扩展一个节点时，选择到目前为止深度最深的节点优先扩展。这一点是在算法的第7步体现出来的。第7步中的ADD（，OPEN）表示将被扩展节点n的所有新子节点 加到OPEN表的前面。开始时，OPEN表中只有一个初始节点s，s被扩展，其子节点被放入OPEN表中。在算法的第3步，OPEN表的第一个元素--设为n--被取出扩展，这时节点n的深度在OPEN表中是最大的，OPEN表中的其他节点的深度都不会超过n的深度。n的子节点被放到OPEN表的最前面。由于子节点的深度要大于父节点的深度，实际上OPEN表是按照节点的深度进行排序的，深度深的节点被排在了前面，而深度浅的节点被放在了后面。这样当下一个循环再次取出OPEN表的第一个元素时，实际上选择的就是到目前为止深度最深的节点，从而实现了深度优先的搜索策略。

　　一般情况下，当问题有解时，深度优先搜索不但不能保证找到最优解，也不能保证一定能找到解。如果问题的状态空间是有限的，则可以保证找到解，当问题的状态空间是无限的时，则可能陷入"深渊"，而找不到解。为此，像回溯算法一样，可以加上对搜索的深度限制。其方法是在算法的第7步，当节点的深度达到限制深度时，则不将其子节点加入到OPEN表中，从而实现对搜索深度的限制。当然，这个深度限制应该设置的合适，深度过深影响搜索的效率，而深度过浅，则可能影响找到问题的解。
　　在介绍回溯策略的时候曾经提到，在有些书上所讲的深度优先实际上指的是我们这里所说的回溯策略，在本书中还是将二者区分开来。从形式上来说，二者确实很相似，所表现出来的都是每次选择深度最深的节点首先扩展。但二者还是有区别的，这里所说的深度优先属于图搜索策略，不足是占用较多的存储空间，好处是对于特殊的问题，可能会提高搜索的效率。

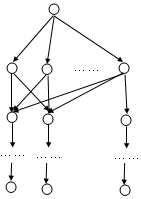
　　设某问题的状态空间如上图所示。从图中可以看出该问题的特点：初始节点有若干个子节点，每个子节点都链接到三条很深的路径中，而目标假定在最右边的路径中。当采用回溯策略时，由于回溯策略只保留从初始节点到当前节点的一条路径，所以从第一个子节点（从左数）进入第一条路径搜索（从左遍数），回溯后，又进入第二条路径。由于没有找到解，又回溯到第二个子节点。从第二个子节点，同样要搜索第一条路径、第二条路径。第三个字节点、第四个子节点……也都同样。这样，第一和第二条路径将被多次搜索，影响了搜索的效率。而对于深度优先策略（单指这里所说的图搜索深度优先），由于保留了所有已经搜索过的路径，当通过第一个节点搜索了第一、第二条路径后，当通过第二个子节点搜索时，由于第一、第二条路径已经被搜索，并且被记录了，所以就不必重复搜索了，提高了搜索的效率。这一点在算法中是如何体现出来的呢？关键是算法的第7步，在n的子节点中，只将类节点加入到了OPEN表中，而对于类节点和类节点则不予考虑。