下面对、、和几类节点通过图例进行说明。

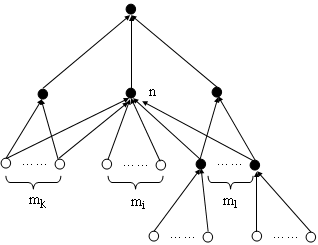
　　如上图所示，假设n是当前被扩展的节点。在n被扩展之前，节点mk和ml已经被生成出来了，其中mk还没有被扩展，他们在OPEN表中，而ml已经被扩展了，他们在CLOSED表中。当n被扩展时，它生成了节点mi，mi由mj、mk和ml三部分组成，其中mj是新出现的节点。

　　这是一个很一般的图搜索过程，通过不断的循环，过程便生成出一个显式表示的图G（搜索图）和一个G的子集T（搜索树）。该搜索树T是由第7步中标记的指针决定，除根节点s外，G中每个节点只有一个指针指向G中的一个父节点，显然树中的每一个节点都处在G中。由于图G是无环的，因此可根据树定义任一条特殊的路径。可以看出，OPEN表上的节点，都是搜索树的端节点，即至今尚未被选作为扩展的节点，而CLOSED表上的节点，可以是已被扩展而不能生成后继节点的那些端节点，也可以是树中的非端节点。

　　图搜索算法，简单地说就是，每次从OPEN表中取出第一个节点进行扩展，生成的新节点放到OPEN表中，然后按照某种原则对OPEN表进行排序。不同的排序原则构成了不同的图搜索算法。值得注意的是算法成功结束的判断方法，是当从OPEN表中取出一个节点后，再判断该节点是否是目标节点，而不是在扩展节点，生成新节点时判断。这一点一定要注意，在后面将可以看到，这是构成某些最优算法的关键所在。
　　这个过程是在第8步要对OPEN表上的节点进行排序，以便在第4步能选出一个"最好"的节点优先扩展。不同的排序方法便可构成形式多样的专门搜索算法，这在后面还要进一步讨论。如果选出待扩展的节点是目标节点，则算法在第5步成功结束，并可根据回溯到s的指针给出解路径。如果某个循环中，搜索树不再剩有待选的节点，即OPEN表变空时，则过程失败结束，问题找不到解。