2．四皇后问题

　　在一个4×4的国际象棋棋盘上，一次一个地摆布四枚皇后棋子，摆好后要满足每行、每列和对角线上只允许出现一枚棋子，即棋子间不许相互俘获。图2.2给出棋盘的几个势态，其中a，b满足目标条件，c，d，e为不合法状态，即不可能构成满足目标条件的中间势态。

图2.2四皇后问题棋盘的几个势态

综合数据库：DATA＝L（表），L的元素。DATA非空时，其表元素表示棋子所在的行和列。因只有4个棋子，故表元素个数最多为4。
图2.2中a，b分别记为（12 24 31 43）和（13 21 34 42），c，d，e分别记为（11 21），（11 22），（11 23 31）等等。
规则集：if 1≤i≤4且Length（DATA）＝i-1
then APPEND （DATA （ij）） （1≤j≤4）
共16条规则，每条规则Rij表示满足前提条件下，在ij处放一棋子。
当规则序列以这种固定排序方式调用BACKTRACK时，四皇后问题的搜索示意图如图2.3所示（为简单起见，每个状态只写出其增量部分）。可以看出，总共回溯22次，主过程结束时返回规则表（）。

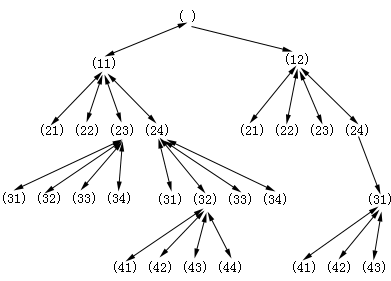
图2.3 固定排序搜索树

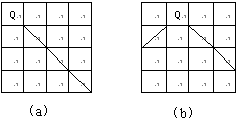
　　在回溯策略中，也可以通过引入一些与问题有关的信息来加快搜索到解的速度。对于皇后问题来说，由于每一行、每一列和每一个对角线，都只能放一个皇后，当一个皇后放到棋盘上后，不管它放在棋盘的什么位置，它所影响的行和列方向上的棋盘位置数是固定的，因此在行、列方面没有什么信息可以利用。但在不同的位置，在对角线方向所影响的棋盘位置数则是不同的，可以想象，如果当把一个皇后放在棋盘的某个位置后，它所影响的棋盘位置数少，那么给以后放皇后留有的余地就大，找到解的可能行也大；反之留有的余地就小，找到解的可能行也小。如下图所示，（a）图皇后所影响的最长对角线是3，而（b）图皇后所影响的最长对角线是2，显然在（b）图位置放置皇后找到解的可能性大于（a）图位置。利用这样的信息对可应用规则集进行动态排序，可以加快找到解的速度。比较图2.3和图2.4，可以说明这种方法对于加快找到解的速度是很有效的。

　　对四皇后问题，如果要利用问题有关信息对规则进行动态排序，则可定义一个对角线函数diag（i，j）。该函数可计算出过棋盘上ij单元的最长的对角线长度，通过比较不同单元的diag（i，j）函数值来决定的排序。如diag（i，k）＜diag（i，j），则为（，），即对角线短的单元，相应的规则排在前面；若diag（i，k）＝diag（i，j），则仍为（，）。由此可计算得规则序列为，这样所得搜索示意图如图2.4所示，利用这样的规则排序方法后，只回溯2次就找到了目标。

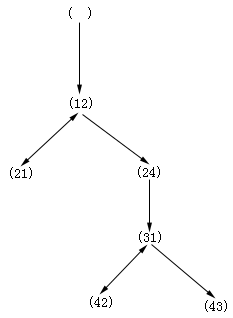
图 2.4 动态排序搜索树