Untitled Document

2.1 回溯策略（Backtracking Strategies）

　　回溯策略属于盲目搜索的一种。所谓回溯策略，简单地说是这样一种策略：首先将规则给出一个固定的排序，在搜索时，对当前状态（搜索开始时，当前状态是初始状态）依次检测每一条规则，在当前状态未使用过的规则中找到第一条可触发规则，被应用于当前状态，得到的新状态重新设置为当前状态，并重复以上搜索。如果当前状态无规则可用，或者所有规则已经被试探过仍未找到问题的解，则将当前状态的前一个状态（即直接生成该状态的状态）设置为当前状态。重复以上搜索，直到找到问题的解，或者试探了所有可能后仍找不到问题的解为止。
　　回溯策略可以有多种实现的方法，其中用递归法实现也许是最简单的方法了，本书中给出的就是这种算法。
　　对于初次接触递归程序设计或者对递归程序设计不熟悉的同学，对这段算法也许不容易理解。在这里对递归程序设计的思想做一个通俗易懂的介绍。对递归程序设计熟悉的同学可以略过。
　　以C语言为例，我们在写一个函数时，一般是用其他已经有的函数（系统提供的库函数或者自己已经定义好的自定义函数）来定义该函数。而递归程序设计则是在定义一个函数时"自己调用自己"（直接的，或者间接的），比如定义abc这个函数，如果写成这样的形式：
int abc(int n)
{
……
abc(m);
……
}
　　则abc是一个递归调用，因为我们在定义abc这个函数时，同时也用到了abc这个函数，这就是所谓的"自己调用自己"。
　　其实我们早就"遇到"过递归了。在大家小的时候，都听过那个"从前有座山……"的故事吧？
"从前有座山，山里有个庙，庙里有个和尚正在讲故事，讲的什么故事呢？讲的是从前有座山，山里有个庙，庙里有个和尚正在讲故事，讲的什么故事呢？讲的是从前有座山，山里有个庙，庙里有个和尚正在讲故事，讲的什么故事呢？讲的是……"
　　这就是一个典型的递归。不过这个递归永远也不会结束，是一种"死递归"。但是我们大家谁也没有"永远"将这个故事听下去。因为当满足一定的条件时，比如讲故事的人口干舌燥不想讲了，故事也就结束了。这虽然是一个一点也不动听的故事，但它确实是一个故事。这里的"口干舌燥"就是递归的一个结束条件，正是由于有了这个条件，才使得递归结束。
　　考察这个故事，有两个特点，一是有一个简单的结束条件，如这里的"口干舌燥"；二是每一次递归调用，都使得问题--在这里就是故事--距离结束近了一些。比如第二次讲"从前有座山"时，就比第一次讲"从前有座山"时距离故事结束近。正是这两点，构成了递归程序设计的两个要点。
　　下面举一个简单的C＋＋程序例子，在这个例子中，利用递归求解一个链表的长度。
struct LIST // 定义一个简单的链表结构
{
LIST *pNext;
};

int ListLenght(LIST *pList)
// 递归定义函数ListLenght
// 函数的功能是求解给定链表的长度
{
if (pList == NULL) return 0;
// 递归的结束条件，一个空的链表长度定义为0
else return ListLenght(pList->pNext)+1;
// 递归调用
// 将求链表pList的长度问题，变换为求解pList->pNext的长度问题
// pList的长度等于pList->pNext的长度+1
}

　　在1.3节中，我们对回溯控制策略作了一般讨论，并以八数码问题为例说明其用法。可以看出求解过程呈现出递归过程的性质，因此用递归算法描述回溯控制下的产生式系统能抓住特点，简单有效。下面定义一个递归过程BACKTRACK，它取单个自变量DATA，设置为产生式系统的综合数据库，若算法成功结束，则返回一张规则表作为解输出；若找不到解，则算法返回FAIL，失败退出。下面用类似LISP语言的形式给出一个具有两个回溯点（即设置两个回溯条件）的简单算法，并通过四皇后问题说明算法的运行过程。

1．递归过程BACKTRACK（DATA）

　　过程BACKTRACK（DATA）的功能是：如果从当前状态DATA到目标状态有路径存在，则返回以规则序列表示的从DATA到目标状态的路径；如果从当前状态DATA到目标状态没有路径存在，则返回FAIL。

递归过程BACKTRACK（DATA）
①IF TERM（DATA），RETURN NIL；TERM取真即找到目标，则过程返回空表NIL。
②IF DEADEND（DATA），RETURN FAIL；DEADEND取真，即该状态不合法，则过程返回FAIL，必须回溯。
③RULES：＝APPRULES（DATA）；APPRULES计算DATA的可应用规则集，依某种原则（任意排列或按启发式准则）排列后赋给RULES。
④LOOP：IF NULL（RULES），RETURN FAIL；NULL取真，即规则用完未找到目标，过程返回FAIL，必须回溯。
⑤R：＝FIRST（RULES）；取头条可应用规则。
⑥RULES：＝TAIL（RULES）；删去头条规则，减少可应用规则表的长度。
⑦RDATA：＝GEN（R，DATA）；调用规则R作用于当前状态，生成新状态。
⑧PATH：＝BACKTRACK（RDATA）；对新状态递归调用本过程。
⑨IF PATH＝FAIL，GO LOOP；当PATH＝FAIL时，递归调用失败，则转移调用另一规则进行测试。
⑩RETURN CONS（R，PATH）；过程返回解路径规则表（或局部解路径子表）。

递归过程BACKTRACK是将循环与递归结合在一起的。下面通过一个示意图，再说明一下该算法的思想。
如下图所示，当前状态n相当于算法中的DATA，（r1，r2，…，ri-1，ri）是n的可应用规则集RULES，m1、m2、…、mi-1、mi是n的i个子状态，它们分别可以通过r1、r2、…、ri-1、ri这i个规则作用于状态n得到。t是目标状态。

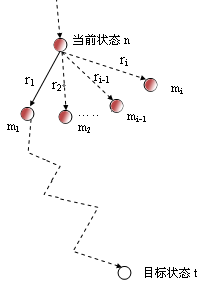
　　为了得到从当前状态n到目标状态t的路径，可以从两个方面考虑。一是要探索n的i个子状态m1、m2、…、mi-1、mi中，通过哪一个状态可以到达目标状态t。这一点，算法是通过循环实现的，每次从n的可应用规则集中，选取一个规则作用于n。所体现的是"横向"探索。二是"纵向"探索。为了探索n的某一个子状态mk（k=1，2，…，i）是否可以达到目标状态t，算法通过递归来完成这个试探。
　　整个算法的思想就是：要想求得从n到t的路径，首先查看m1到t是否有路径存在。如果从m1到t有路径存在，则在该路径前加上r1，就得到了从n到t的路径（这里的路径是用规则的集合表示的）。在试探m1到t有没有路径的过程中，m1又成为了当前状态，又要探索m1的子状态到t是否有路径存在，如此进行下去。递归所起的正是这样的作用。如果从m1到t没有路径存在，算法则试探m2到t是否存在路径，它同样也要试探m2的子状态到t有无路径存在，等等。所以算法中循环和递归是交叉进行的，一方面是"横向"探索，一方面是"纵向"探索。

　　下面对这个算法作几点说明。首先解释一下其中的变量、常量、谓词、函数等符号的意义。变量符号DATA、RULES、R、RDATA、PATH分别表示当前状态、规则集序列表、当前调用规则、新生成状态、当前解路径表。常量符号NIL、FAIL、LOOP分别表示空表、回溯点标记、循环标号。当状态变量DATA满足结束条件时，TERM（DATA）取真；当DATA为非法状态时，DEADEND（DATA）取真；当规则集变量表RULES取空时，NULL取真。函数RETURN、APPRULES、FIRST、TAIL、GEN、GO、CONS的作用是：RETURN返回其自变量值；APPRULES求可应用规则集；FIRST和TAIL分别取表头和表尾；GEN调用规则R生成新状态；GO执行转移；CONS构造新表，把其第一个自变量加到一个表（第二个自变量）的前头。BACKTRACK（RDATA）表示调用递归过程作用于新自变量上。
　　这里再说明一下该过程的运行情况。当某一个状态Sg满足结束条件时，算法才在第1步结束并返回NIL，此时BACKTRACK（Sg）＝NIL。失败退出发生在第2、4步，第2步是处理不合法状态的回溯点，而第4步是处理全部规则应用均失败时的回溯点。若处在递归调用过程期间失败，过程会回溯到上一层继续运行，而在最高层失败则整个过程宣告失败退出。构造成功结束时的规则表在第10步完成。算法第3步实现可应用规则的排序，可以是固定排序或根据启发信息排序。

　　这个简单的BACKTRACK过程只设置两个回溯点，可用于求解N－皇后这类性质的问题，下面以四皇后问题为例来说明算法的运行过程。