一般地，很多问题可以转化为状态空间的搜索问题。
　　比如传教士和野人问题，当我们用在河的左岸的传教士人数、野人人数和船的情况表示问题时，该问题的初始状态可以用三元组表示为（3，3，1），结束状态可以表示为（0，0，0），而中间状态则可以表示为（2，2，0）、（3，2，1）、（3，0，0）……等，每个三元组对应了三维空间上的一个点，而问题的解，则是一个合法状态的序列，其中序列的第一个状态是问题的初始状态，而最后的一个状态则是问题的结束状态。介于初始状态和结束状态之间的则是中间状态。除了第一个状态外，该序列中任何一个状态，都可以通过一条规则，由与他相邻的前一个状态转换得到。
　　问题的解也可以用规则的序列表示，该序列由上述状态序列的转化规则，按顺序组成。
　　有时问题的解，又可以称为解路径。
　　一般来说，问题的规模（问题所有可能出现的状态数）是比较大的，就拿8数码问题这样一个并不太复杂的问题来说，其规模就达到9！＝362880个状态。当问题有解时，如何缩小查找范围，快速有效地找到问题的解，甚至是问题的最优解，正是搜索所要讨论的问题。

　　上一章讨论用产生式系统求解问题的过程中，已涉及到几种搜索策略的基本思想，当所给定的问题用状态空间表示时，则求解过程可归结为对状态空间的搜索。从图2.1表示出的搜索过程可以看出，当问题有解时，使用不同的搜索策略，找到解的搜索空间范围是有区别的。一般来说，对大空间问题，搜索策略是要解决组合爆炸的问题。

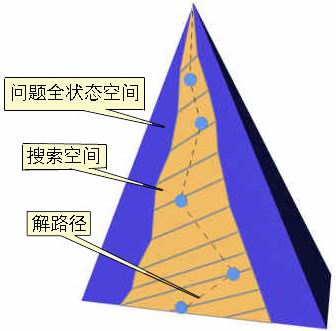
图2.1搜索空间示意图

　　从搜索方式上来讲，搜索可以划分为两大类，即盲目搜索和启发式搜索。
　　所谓盲目搜索，就是未利用问题的知识，采用固定的方式生成状态的方法。显然这种方法的搜索效率是低下的，但方法具有通用性。当一时难以找到求解问题的有效知识时，是一种不得不采用的方法。
　　所谓启发式搜索，与盲目搜索正好相反，它利用问题的知识，缩小问题的搜索范围，选择那些最有可能在（最优）解路径上的状态优先搜索，以尽快地找到问题的（最优）解。由于利用了问题的有关知识，一般来说，搜索效率会有所提高。但如何找到对求解问题有帮助的知识，以及如何利用这些知识，是问题的关键所在。
本章所要的讨论的问题如下：
　*有哪些常用的搜索算法。
　*问题有解时能否找到解。
　*找到的解是最佳的吗？
　*什么情况下可以找到最佳解？
　*求解的效率如何。

　　通常搜索策略的主要任务是确定如何选取规则的方式。有两种基本方式：一种是不考虑给定问题所具有的特定知识，系统根据事先确定好的某种固定排序，依次调用规则或随机调用规则，这实际上是盲目搜索的方法，一般统称为无信息引导的搜索策略。另一种是考虑问题领域可应用的知识，动态地确定规则的排序，优先调用较合适的规则使用，这就是通常称为启发式搜索策略或有信息引导的搜索策略。
到目前为止，在人工智能领域中已提出许多具体的搜索方法，概括起来有：
（1）求任一解路的搜索策略
　　回溯法（Backtracking）
　　爬山法（Hill Climbing）
　　宽度优先法（Breadth-first）
　　深度优先法（Depth-first）
　　限定范围搜索法（Beam Search）
　　好的优先法（Best-first）
（2）求最佳解路的搜索策略
　　大英博物馆法（British Museum）
　　分枝界限法（Branch and Bound）
　　动态规划法（Dynamic Programming）
　　最佳图搜索法（A�~）
（3）求与或关系解图的搜索法
　　一般与或图搜索法（AO�~）
　　极小极大法（Minimax）
　　α－β剪枝法（Alpha-beta Pruning）
　　启发式剪枝法（Heuristic Pruning）
本章及下一章仅对其中几个基本搜索策略作进一步的讨论。