3．可分解的产生式系统

　　如果一个产生式系统可以分解为几个子问题，当子问题得以求解时，则原始问题被求解。这样的产生式系统称为可分解的产生式系统。可分解的产生式系统如果原始问题可以被划分为几个独立的子问题来求解，则可以提高问题求解的效率。但在很多情况下，子问题之间并不是完全独立的，它们之间会有某些方面的联系，这样的可分解产生式系统可以表示为一个与或树（图）。有关与或树（图）的求解问题将在第三章介绍。

我们来研究一个重写问题的产生式系统，其初始数据库为（C，B，Z），产生式规则的依据是如下的重写规则：
R1：C→（D，L）
R2：C→（B，M）
R3：B→（M，M）
R4：Z→（B，B，M）
结束条件是生成出只包含M组成的数据库，即（M，…，M）。
用图搜索方式求解这个问题时，搜索得到的部分状态空间图如图1.14所示。图中只给出两条达到目标的路径和一条失败的路径。实际搜索时有可能去探索更多的路径，往往导致效率降低。

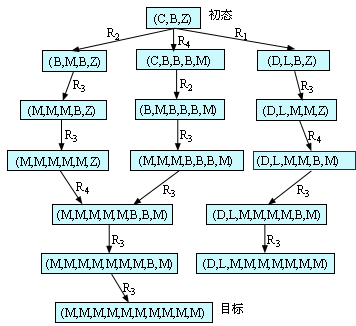
图1.14重写问题部分搜索图

　　对于这个问题，为了避免搜索多余的路径，可将初始数据库分解成几个可以独立加以处理的分量，分别对它们进行求解。即可分别对每一个分量数据库，测试产生式规则可应用的条件，然后应用于每一个分量生成出新的数据库，如此分解、生成交替进行下去，直到分量数据库满足某种结束条件为止。要注意一般结束条件也应分解为对应于分量数据库所使用的结束条件。
能够分解产生式系统的综合数据库和结束条件的产生式系统称为可分解的产生式系统。一个可分解的产生式系统，其基本过程描述如下：
过程 SPLIT
（1）DATA:＝初始数据库
（2）{Di}:＝DATA的分解式；每个Di元素都看成单独的数据库
（3）Until {Di}的所有元素都满足结束条件之前，do：
（4）begin
（5） 从{Di}中选一个不满足结束条件的D*
（6） 从{Di}中删去D*
（7） 在规则集中选择一条可应用于D*的规则R
（8） D:＝R应用于D*的结果
（9） {di}:＝D的分解式
（10） 在{Di}上添加di
（11）end

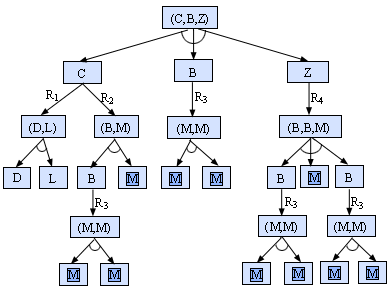
图1.15重写问题的与或树

　　SPLIT的控制策略是要在第5步选一个分量数据库，在第7步选一条可应用于D*的规则R，显然为满足结束条件，在{}中不满足结束条件的元素，最终都必须选择到，而对任一选出的，可以只考虑选择一条可应用的规则使用。至于分量数据库具体排序方法以及处理分量数据库时规则选取的策略，一般应根据具体问题进行考虑。当采用图搜索方式求解可分解产生式系统时，用一种与或图（树）结构来表示是很清晰的。图1.15给出上述重写问题的与或树表示，它和一般的有向图类似，图中的节点代表综合数据库，有向弧组（有小段圆弧链结）表示复合数据库和分解后的各分量数据库之间具有的与关系。即其后继节点（分量数据库）的集合中全部分量都处理完毕，复合数据库才算处理完，我们称这些后继节点为与节点。同样其余有向弧可表示某个分量数据库和应用规则之后产生的新数据库之间具有的或关系，因为在这几个后继节点中（即新数据库，又可能再被分解）只要有一个处理完毕，这个分量数据库就算处理完，我们称这些后继节点为或节点。此外图中双线框表示的那些节点称为终节点，这些节点代表的分量数据库满足结束条件（符号M）。
　　重写问题的解可以用与或图中某一子图来表示，图1.15中粗线弧表示出的那一部分子图就代表一个解图，其"端节点"所对应的数据库，每一个都满足结束条件。解图的一般搜索算法第三章再详细讨论。