2．可交换的产生式系统

　　可交换的产生式系统，简单的说，指的是这样一类产生式系统，问题的求解与规则的使用次序无关。规则的使用次序只可能影响到求解的效率，不影响是否能得到问题的解。在本课程后面将要讲到的谓词逻辑的归结方法，从产生式系统的角度来看，就是一个典型的可交换的产生式系统。

　　下面分析一下图1.12所示的一个简单的状态空间图。

图1.12简单的状态空间图

　　图中是初始状态，Sg是目标状态，可应用于的规则集{}对状态空间其他任一状态都可以应用，也就是说对生成的新状态，这三条规则仍然适用，同样对它们的后裔也是这样。此外，还可以看出从到达目标Sg解序列与这三条规则的使用次序无关。具有这些性质的系统称为可交换产生式系统，可交换性是指这种情况下这几条规则可以任意交换次序而不影响求解。但要注意并不是所使用的整个规则序列可以重新排列，只有那些最初可应用于初始数据库的规则才可交换，而对于生成的数据库所添加的其他可应用规则，则不能随意交换。
一般来说，当一个产生式系统对任何一个数据库D都具有如下性质时，这个产生式系统是可交换的：
（1）可应用于D的规则集合，对用了其中任意一条规则之后所生成的任何数据库，这个规则集合还适用；
（2）满足目标条件的某个数据库D，当应用任何一个可应用于数据库D的规则之后所生成的任何数据库，仍然满足目标条件；
（3）若对D应用某一规则序列之后得到一个数据库D′（设有一对应于D→D′的一条解路），则当改变D的可应用规则集合中的规则次序后，仍然可求得解，即求得D′与使用满足D的可应用规则集合中的规则次序无关。

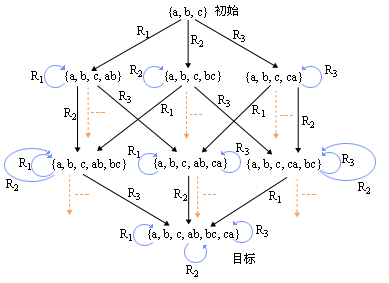
图1.13整数集合生成问题的部分状态空间图

　　下面分析一个可交换性的简例。给定一个整数集合{a，b，c}，可通过把集合中任意一对元素的乘积作为新元素添加到集合中的办法来扩大该整数集，要求通过若干次操作后能生成出所需的整数集合来。用产生式系统求解这个问题，其综合数据库就可用集合表示，则问题的初始状态为{a，b，c}，设目标条件为具有a，b，c，ab，bc，ca这六个元素组成的集合，初始状态可应用的规则集合为

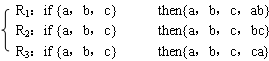
　　显然，这个产生式系统具有上述三个性质，具有可交换性，其部分状态空间图如图1.13所示。
　　由于具有可交换性，求解时只需搜索其中任意一条路径，只要解存在就一定能找到目标，不必探索多条路径，因此不可撤回的控制方式在这种系统中使用很合适，因解与最初可应用的规则的次序无关，系统不必提供特殊选择规则的机理。