上述的PRODUCTION过程中，如何选择一条可应用的规则，作用于当前的综合数据库，生成新的状态以及记住选用的规则序列是构成控制策略的主要内容。对大多数的人工智能应用问题，所拥有的控制策略知识或信息并不足以使每次通过算法第4步时，一下子就能选出最合适的一条规则来，因而人工智能产生式系统的运行就表现出一种搜索过程，在每一个循环中选一条规则试用，直至找到某一个序列能产生一个满足结束条件的数据库为止。由此可见高效率的控制策略是需要有关被求解问题的足够知识，这样才能在搜索过程中减少盲目性，比较快地找到解路径。
1．分类
控制策略可划分为两大类：

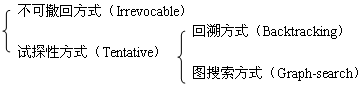
下面举例说明这几种策略的基本思想。

图1.4 爬山过程示意图

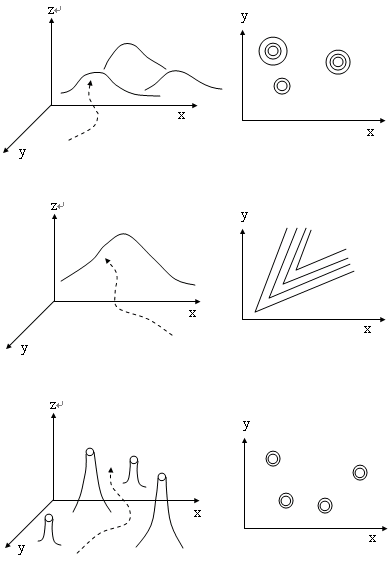
图1.5复杂情况出现的问题

（1）不可撤回方式：这种方式是利用问题给出的局部知识来决定如何选取规则，就是说根据当前可靠的局部知识选一条可应用规则并作用于当前综合数据库。接着再根据新状态继续选取规则，搜索过程一直进行下去，不必考虑撤回用过的规则。这是由于在搜索过程中如能有效利用局部知识，即使使用了一条不理想的规则，也不妨碍下一步选得另一条更合适的规则。这样不撤消用过的规则，并不影响求到解，只是解序列中可能多了一些不必要的规则。显然这种策略具有控制简单的优点，下面用登山问题来进一步说明这种方式的基本思想。
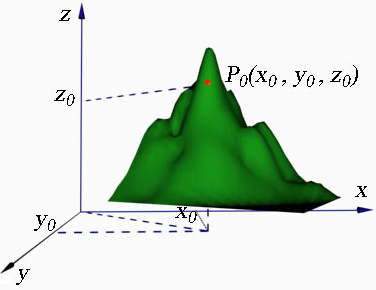
　　人们在登山过程中，目标是爬到峰顶，问题就是确定如何一步一步地朝着目标前进达到顶峰。其实这就是一个"爬山"过程中寻求函数的极大值问题。我们很容易想到利用高度随位置变化的函数H（P）来引导爬山，就可实现不可撤回的控制方式。
　　图1.4表示出登山运动员当前所处某一位置，如果规定好有四种走法[向东（Δx）、向西（－Δx）、向北（Δy）、向南（－Δy）迈出一步，这相当于有4条规则]，那么这时可以用H（P）计算一下不同方向时高度变化的情况，即求出Δz1＝H（Δx）、Δz2＝H（－Δx）、Δz3＝H（Δy）、Δz4＝H（－Δy），然后选择Δz变化最大的那个走向攀登一步，进入一个新的位置P，即在梯度最陡的方向前进一步。然后从P开始重复这一过程直至到达某一点为止，这一点就是顶峰点，再进行试探都会导致高度的下降。因此这种策略又称为爬山法。
　　用不可撤回的方式（爬山法）来求解登山问题，只有在登单峰的山时才总是有效的（即对单极值的问题可找到解）。对于比较复杂的情况，如碰到多峰、山脊或平顶的情况时，爬山搜索法并不总是有效的。图1.5示出这些情况下可能遇到的问题。可以看出，多峰时如果初始点处在非主峰的区域，则只能找到局部优的点上，即得到一个虚假的实现了目标的错觉。对有山脊的情况，如果搜索方向与山脊的走向不一致，则就会停留在山脊处，并以为找到极值点。当出现大片平原区把各山包孤立起来时，就会在平顶区漫无边际的搜索，总是试验不出度量函数有变化的情况，这导致了随机盲目的搜索。
　　下面看一看如何运用爬山过程的思想使产生式系统具有不可撤回的控制方式。首先要建立一个描述综合数据库变化的函数，如果这个函数具有单极值，且这个极值对应的状态就是目标，则不可撤回的控制策略就是选择使函数值发生最大增长变化的那条规则来作用于综合数据库，如此循环下去直到没有规则使函数值继续增长，这时函数值取最大值，满足结束条件。
　　我们举八数码游戏的例子加以说明。用"不在位"将牌个数并取其负值作为状态描述的函数－W（n）（"不在位"将牌个数是指当前状态与目标状态对应位置逐一比较后有差异的将牌总个数，用W（n）表示，其中n表示任一状态），例如图1.1中的初始状态，其函数值是-4，而对目标状态，函数值是0。用这样定义的函数就能计算出任一状态的函数值来。
　　从初始状态出发看一看如何应用这个函数来选取规则。对初始状态，有三条可应用规则，空格向左和空格向右这两规则生成的新状态，其－W（n）均为－5，空格向上所得新状态，其－W（n）＝－3，比较后看出这条规则可获得函数值的最大增长，所以产生式系统就选择这条规则来应用。按此一步步进行下去，直至产生式系统结束时就可获得解。图1.6表示出求解过程所出现的状态序列，图中画圆圈的数字就是爬山函数值。从图中还可看出，沿着状态变化路径，出现有函数值不增加的情况，就是说出现了没有一条合适的规则能使函数值增加，这时就要任选一条函数值不减小的规则来应用，如果不存在这样的规则，则过程停止。
　　从图1.6中所示的情况来看，用爬山策略（不可撤回）能找到一条通往目标的路径。然而一般说来，爬山函数会有多个局部的极大值情况，这样一来就会破坏爬山法找到真正的目标。例如初始状态和目标状态分别如下：

　　任意一条可应用于初始状态的规则，都会使－W（n）下降，这相当于初始状态的描述函数值处于局部极大值上，搜索过程停止不前，找不到代表目标的全局极大值。
根据以上讨论看出，对人工智能感兴趣的一些问题，使用不可撤回的策略，虽然不可能对任何状态总能选得最优的规则，但是如果应用了一条不合适的规则之后，不去撤消它并不排除下一步应用一条合适的规则，那末只是解序列有些多余的规则而已，求得的解不是最优解，但控制较简单。此外还应当看到，有时很难对给定问题构造出任何情况下都能通用的简单爬山函数（即不具多极值或"平顶"等情况的函数），因而不可撤回的方式具有一定的局限性。