（2）规则集合：由摆渡操作组成。该问题主要有两种操作：操作（规定为从左岸划向右岸）和操作（从右岸划向左岸）。每次摆渡操作，船上人数有五种组合，因而组成有10条规则的集合。

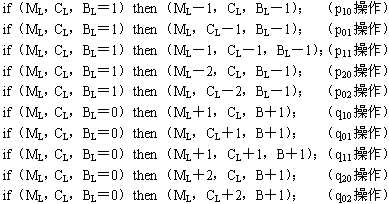
（3）初始和目标状态：即（3，3，1）和（0，0，0）。
　　和八数码游戏的问题一样，建立了产生式系统描述之后，就可以通过控制策略，对状态空间进行搜索，求得一个摆渡操作序列，使其能够达到目标状态。
　　在讨论用产生式系统求解问题时，有时引入状态空间图的概念很有帮助。状态空间图是一个有向图，其节点可表示问题的各种状态（综合数据库），节点之间的弧线代表一些操作（产生式规则），它们可把一种状态导向另一种状态。这样建立起来的状态空间图，描述了问题所有可能出现的状态及状态和操作之间的关系，因而可以较直观地看出问题的解路径及其性质。实际上只有问题空间规模较小的问题才可能作出状态空间图，例如N＝3的M－C问题，其状态空间图如图1.3所示。由于每个摆渡操作都有对应的逆操作，即对应，所以该图也可表示成具有双向弧的形式。
　　从状态空间图看出解序列相当之多，但最短解序列只有4个，均由11次摆渡操作构成。若给定其中任意两个状态分别作为初始状态和目标状态，就立即可找出对应的解序列来。在一般情况下，求解过程就是对状态空间搜索出一条解路径的过程。
　　以上两个例子说明了建立产生式系统描述的过程，这也就是所谓问题的表示。对问题表示的好坏，往往对求解过程的效率有很大影响。一种较好的表示法会简化状态空间和规则集表示，例如八数码问题中，如用将牌移动来描述规则，则8块将牌就有32条的规则集，显然用空格走步来描述就简单得多。又如M－C问题中，用3×2的矩阵给出左、右岸的情况来表示一种状态当然可以，但显然仅用描述左岸的三元组描述就足以表示出整个情况，因此必须十分重视选择较好的问题表示法。以后的讨论还可以看到高效率的问题求解过程与控制策略有关，合适的控制策略可缩小状态空间的搜索范围，提高求解的效率。

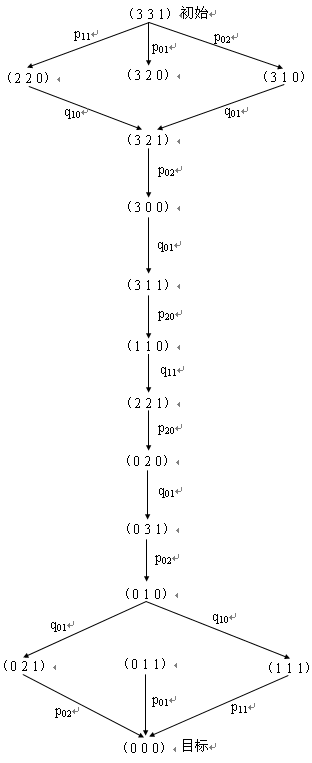
图1.3 M－C问题状态空间图