2．传教士和野人问题（Missionaries and Cannibals）
传教士和野人问题是一个经典的智力游戏问题。在这个问题中，实际上隐含了这样一个条件：如果在河的某一岸只有野人，而没有传教士，也同样被认为是合法状态。在具体书写某些条件时，为了简便，这一点有时并没有考虑，但我们默认这个条件是被考虑了的。
有N个传教士和N个野人来到河边准备渡河，河岸有一条船，每次至多可供k人乘渡。问传教士为了安全起见，应如何规划摆渡方案，使得任何时刻，在河的两岸以及船上的野人数目总是不超过传教士的数目。即求解传教士和野人从左岸全部摆渡到右岸的过程中，任何时刻满足M（传教士数）≥C（野人数）和M＋C≤k的摆渡方案。
设N＝3，k＝2，则给定的问题可用图1.2表示，图中L和R表示左岸和右岸，B＝1或0分别表示有船或无船。约束条件是：两岸上M≥C，船上M＋C≤2。
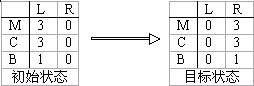
图1.2 M－C问题实例
由于传教士和野人数是一个常数，所以知道了一岸的情况，另一岸的情况也就知道了。因此为了简便起见，在描述问题时，只描述一岸--如左岸--的情况就可以了。
另外，该问题我们最关心的是在摆渡过程中，两岸状态的变化情况，因此船上的情况并不需要直接表达出来。在一次摆渡过程中，船上究竟有几个传教士和野人，可以通过两个相连的状态简单得到。这样表达更简练，突出了问题的重点。
（1）综合数据库：用三元组表示左岸的情况，即
（
，
，
），其中0≤，≤3，∈{0，1}，其中表示在左岸的传教士人数，表示在左岸的野人数，＝1表示船在左岸，＝0表示船在右岸。则此时问题描述可以简化为：
（3，3，1）→（0，0，0）
在描述实际问题时，并不要求给出这些具体的状态分析，而且由于实际问题的复杂性，也不可能得到这么详细的状态分析。这里给出状态分析的目的，是为了读者通过该例子，了解都有哪些类型的状态。其中"不合法"状态是那些不满足问题要求的状态，"达不到"状态是一些"孤立"状态，它不可能通过一个合法状态达到。
N＝3的M－C问题，状态空间的总状态数为4×4×2＝32，根据约束条件的要求，可以看出只有20个合法状态。再进一步分析后，又发现有4个合法状态实际上是不可能达到的。因此实际的问题空间仅由16个状态构成。下表列出分析的结果：
| （
）
（ 0 0 1）达不到 （ 0 1 1） （ 0 2 1） （ 0 3 1） （ 1 0 1）不合法 （ 1 1 1） （ 1 2 1）不合法 （ 1 3 1）不合法 （ 2 0 1）不合法 （ 2 1 1）不合法 （ 2 2 1） （ 2 3 1）不合法 （ 3 0 1）达不到 （ 3 1 1） （ 3 2 1） （ 3 3 1） |
（
） （ 0 0 0） （ 0 1 0） （ 0 2 0） （ 0 3 0）达不到 （ 1 0 0）不合法 （ 1 1 0） （ 1 2 0）不合法 （ 1 3 0）不合法 （ 2 0 0）不合法 （ 2 1 0）不合法 （ 2 3 0）不合法 （ 3 0 0） （ 2 2 0） （ 3 1 0） （ 3 2 0） （ 3 3 0）达不到 |
规则集可以划分为两组：一组是从左岸到右岸，称为p操作，另一组是从右岸到左岸，称为q操作。按道理，在规则的前件中应该附加必要的条件，使得产生的状态是合法的。在下一章有关搜索算法的讨论中我们会看到，在每一种搜索算法中，都有一处判断新产生的状态是否合法。对于不合法的状态，算法会进行相应的处理。因此在表达规则时，那些通过状态的合法性就可以判断的前提条件可以不在规则中出现。这样可以简化规则的表达。比如在第一条规则中，在规则后件中出现了"ML－1"，按道理应该要求ML>0，否则的话，在左岸的传教士人数就是负数了。但这一点完全可以通过定义什么是合法状态来判断，因此就没有必要将这个条件写入规则中了。但为什么在规则中写入"BL＝1"、"B＝0"这样的条件呢？其实这样的条件也不是一定要写的，因为它同样可以通过定义合法状态来判断。但由于写上这些条件后，会使得规则表达更清晰，通过BL的取值就可以看出规则所表达的是船从左岸到右岸，还是从右岸到左岸。而且从左到右，或者从右到左，是交替进行的，因此把这样的条件明确表达出来，可以提高问题的求解效率。所以说，对于通过状态的合法性可以判断的条件，是否在规则中明确表达出来，具有一定的灵活性，可以从规则的清晰性、易懂性，以及求解效率等方面综合考虑。而对于某些不能通过状态的合法性来判断的条件，则必须在规则中明确表达出来。
在传教士和野人问题中，假定了传教士和野人都可以划船，由于每次摆渡船上最多可以有2个人，最少也必须有一个人（船不会自己前进），因此在船上共有（2，0）、（0，2）、（1，1）、（1，0）和（0，1）这5种组合。其中第一个数字表示在船上的传教士数，第二个数字表示在船上的野人数。再加上从左岸到右岸和从右岸到左岸这两种情况，所以共有10种摆渡方法。在该例题中，将这10种摆渡方法全部以规则的形式，一一列举出来。这种方法的好处是，规则简单、易懂，但不足也很明显：繁琐。尤其是对于实际的复杂问题，如果要全部一一列举出所有规则，其数量太大。表示规则的另一种方式就是引入变量，通过引入变量，将相近的几条规则组合在一条规则中表示。同样是传教士和野人问题，我们引入i和j两个变量，分别表示此次摆渡时，过河的传教士数和野人数，则可以将10条规则组合为两条规则：
IF (m, c, 1) AND 1≤i+j≤2 THEN (m-i, c-j, 0)
IF (m, c, 0) AND 1≤i+j≤2 THEN (m+i, c+j, 0)
（也可以表示为：
IF (m, c, b=1) AND 1≤i+j≤2 THEN (m-i, c-j, b-1)
IF (m, c, b=0) AND 1≤i+j≤2 THEN (m+i, c+j, b+1)
）
这样表达的规则更加精练，但程序设计要复杂的多，因为需要对变量进行解释。