产生式系统最初并不是针对人工智能问题提出的。正象在课前思考中提到的那样，人们在研究人工智能问题时，发现产生式系统可以比较好的模拟人类推理的思维过程。所以在建造人工智能系统时，人们将产生式系统引入过来，用于建立人类认知的模型。产生式系统形式上虽然很简单，但在一定意义上模仿了人类思考的过程。最初的专家系统，就是建立在产生式系统这种结构之上的，后来的专家系统虽然有了很大的发展，但其基本模式仍然没有改变。

1.1　产生式系统的组成部分

　　综合数据库、产生式规则集和控制系统，被称为产生式系统的三要素。这里的综合数据库，只是借用了数据库这样一个名词，与我们通常所说的数据库概念并不一致。它是一个数据的集合，用于存放在推理过程中的已知条件、推导出的中间结果和最终结论等。一组产生式规则（规则集）相当于系统的知识库，它采用"IF <前件> THEN <后件>"的形式，来表达求解问题所需要的知识。其中规则的<前件>表达的是该条规则所要满足的条件，规则的<后件>表示的是该规则所得出的结论，或者动作。规则表达的可以是与待求解的问题有关的客观规律方面的知识，也可以是对求解问题有帮助的策略方面的知识。以中国象棋为例，前者描述的是象棋的走棋规则，如"马走日"、"象走田"等。这是系统所必须表达出来的知识。而后者描述的则是在什么情况下，应该如何走棋才能战胜对手，或者什么样的局面比较有力，什么样的局面不利等。这方面的知识与搜索结合在一起，决定了系统下棋的水平。控制系统，又称为控制策略或者搜索策略，用于控制系统的运行，它根据综合数据库中的当前数据，来选择合适的规则。不同的选择规则的方法，就构成了不同的控制策略。因此，控制系统也可以称之为推理引擎。
　　一个人工智能产生式系统的基本要素是：一个综合数据库（Globle Database）；一组产生式规则（Set of Rules）和一个控制系统（Control System）。
综合数据库是人工智能产生式系统所使用的主要数据结构，它用来表述问题状态或有关事实，即它含有所求解问题的信息，其中有些部分可以是不变的，有些部分则可能只与当前问题的解有关。人们可以根据问题的性质，用适当的方法来构造综合数据库的信息。
产生式规则的一般形式为
条件----> 行动 　或 　前提----> 结论　　
即表示成为
if……then……
的形式。其中左半部确定了该规则可应用的先决条件，右半部描述了应用这条规则所采取的行动或得出的结论。一条产生式规则满足了应用的先决条件之后，就可对综合数据库进行操作，使其发生变化。如综合数据库代表当前状态，则应用规则后就使状态发生转换，生成出新状态。
控制系统或策略（Control Strategies）是规则的解释程序。它规定了如何选择一条可应用的规则对数据库进行操作，即决定了问题求解过程的推理路线。当数据库满足结束条件时，系统就应停止运行；还要使系统在求解过程中记住应用过的规则序列，以便最终能给出解的路径。
上述产生式系统的定义具有一般性，它可用来模拟任一可计算过程。在研究人类进行问题求解过程时，完全可用一个产生式系统来模拟求解过程，即可作为描述搜索的一种有效方法。作为人工智能中的一种形式体系，它还具有以下优点：

产生式系统的特点可以概括为：
1，数据驱动。系统是在数据的驱动下运行的，数据一旦发生变化，如增加数据、删除数据等，就会导致系统行为的变化。而一旦数据不再发生变化，系统的运行也就停止了。
2，独立性。独立性包含两方面的含义。其一是说，数据（综合数据库）、知识（规则集）和控制（控制系统），三者之间是相互独立的，而不是混杂在一起的。其二是说，规则之间是相互独立的，不同的规则之间没有明显的连接关系，规则之间是通过数据联系在一起的。这样可以便于规则集的维护，一条规则的修改或者增删，不需要考虑它与哪些规则相关联。由于规则之间是相互独立的，因此一般来说，问题的求解与规则的排列顺序无关。

（1）适合于模拟强数据驱动特点的智能行为。当一些新的数据输入时，系统的行为就要改变。
（2）易于添加新规则去适应新的情况，而不会破坏系统的其他部分。这是由于产生式系统的各组成部分具有相对的独立性，因而便于扩展和修改。
下面举例说明如何用产生式系统来描述或表示求解的问题，即如何对具体的问题建立起产生式系统的描述，以及用产生式系统求解问题的基本思想。
1．八数码游戏（Eight－Puzzle）
　　在3×3组成的九宫格棋盘上，摆有八个将牌，每一个将牌都刻有1-8数码中的某一个数码。棋盘中留有一个空格，允许其周围的某一个将牌向空格移动，这样通过移动将牌就可以不断改变将牌的布局。这种游戏求解的问题是：给定一种初始的将牌布局或结构（称初始状态）和一个目标的布局（称目标状态），问如何移动将牌，实现从初始状态到目标状态的转变。问题的解答其实就是给出一个合法的走步序列。
要用产生式系统来求解这个问题，首先必须建立起问题的产生式系统描述，即规定出综合数据库、规则集合及其控制策略。这种把一个问题的叙述转化为产生式系统的三个组成部分，在人工智能中通常称为问题的表示。一般来说一个问题可有多种表示方式，而选择一种较好的表示是运用人工智能技术解决实际问题首先要考虑的，而且要有一定的技巧。
设给定的具体问题如图1.1所示。

（1）综合数据库：在这里是要选择一种数据结构来表示将牌的布局。通常可用来表示综合数据库的数据结构有符号串、向量、集合、数组、树、表格、文件等。对八数码问题，选用二维数组来表示将牌的布局很直观，因此该问题的综合数据库可以如下形式表示：
（），其中1≤i、j≤3，∈{0，1，…，8}，且互不相等。这样每一个具体的矩阵就可表示一个棋局状态。对八数码游戏，显然共有9!＝362880个状态。所有可能的状态集合就构成该问题的状态空间或问题空间。可以证明八数码问题的实际问题空间只有。

　　八数码问题实际上是将牌在移动，但将牌的移动也可以看成是空格的移动。由于空格只有一个，因此表示起来更方便。
　　在书写规则集的时候，要求规则集要完整，把与问题有关的规则都要表达出来。在做练习的时候，有些问题可能比较简单，一下就知道了问题的答案。初学者这时容易犯的错误就是，根据解答来书写规则集，只表达出那些在求解过程中用到的规则。这是不全面的，因为有些规则在当前给定的条件下可能用不到，一旦改变了问题的初始条件，就可能用到，所表达的规则集不能因为初始条件不同而不同。而且在实际问题中，一般来说问题都比较复杂，事先不可能知道哪些规则用得到，哪些规则用不到，因此要求把有关的规则尽可能的表达全面，以提高系统求解问题的能力。当然，由于实际问题的复杂性，要全面表达出全部规则也不是一件容易的事。这需要在使用当中，逐步完善规则集。

（2）规则集合：移动一块将牌（即走一步）就使状态发生转变。改变状态有4种走法：空格左移、空格上移、空格右移、空格下移。这4种走法可用4条产生式规则来模拟，应用每条规则都应满足一定的条件。于是规则集可形式化表示如下：
设记矩阵第i行第j列的数码，记空格所在的行、列数值，即，则

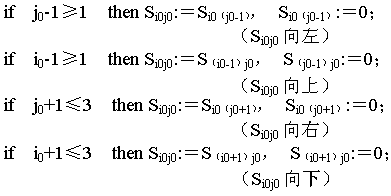
控制策略（搜索策略）决定了产生式系统求解问题时所采用的搜索方法，一般来说，是某种算法。在后面我们会学到"深度优先"、"宽度优先"等搜索算法，在这里暂时先不考虑。

（3）搜索策略：是从规则集中选取规则并作用于状态的一种广义选取函数。确定某一种策略后，可以算法的形式给出。

　　在用产生式系统描述一个问题时，除了产生式系统的三要素外，一般还要求给出问题的初始状态和结束状态（目标状态）。初始状态和结束状态要求采用与综合数据库相同的结构表达。如在八数码问题中，如果综合数据库采用矩阵的结构，则一个初始条件可以表达为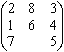 ，而结束状态可以表达为 。如果综合数据库采用一个字符串　　来表达，比如从矩阵的左上角开始，按顺时针遍历每一个将牌，中间一个位置在最后，其中空格用0表示，则相同的初始状态可以表达为"283450716"，而结束状态可以表达为"123456780"。有时候，目标并不是一个状态，而是要求满足一定的条件。如在八数码问题中，如果目标只要求空格在中间位置，则综合数据库采用矩阵结构时，结束条件可以表达为：。其中0表示空格。

　　在建立产生式系统描述时，还要给出初始状态和目标条件，具体说明所求解的问题。产生式系统中控制策略的作用就是从初始状态出发，寻求一个满足一定条件的问题状态。对该八数码问题，初始状态可表示为 ；目标描述可表示为 ，它是一种显式表示的描述。更一般的情况可以是规定出达到目标的某个真／假条件的描述，如规定要达到第一行将牌数码总和为6的状态。显然这样一个条件，隐含地确定了目标是一个状态的子集---目标集。目标条件也是产生式系统结束条件的基础。

　　如何求解一个用产生式系统描述的问题，以及如何寻找具有最小耗散的解，属于搜索策略问题，在下一章将介绍有关的经典算法。

　　建立了产生式系统描述之后，通过控制策略，可求得实现目标的一个走步序列（即规则序列），这就是所谓的问题的解，如走步序列（上、上、左、下、右）就是一个解。这个解序列是根据控制系统记住搜索目标过程中用过的所有规则而构造出来的。
　　在一般情况下，问题可能有多个解的序列，但有时会要求得到有某些附加约束条件的解，例如要求步数最少、距离最短等。这个约束条件通常是用耗散或代价（cost）这一概念来概括，这时问题可提为寻找具有最小耗散的解。
　　现在再来看一下人们是如何来求解八数码游戏的。首先是仔细观察和分析初始的棋局状态，通过思考决定走法之后，就移动某一块将牌，从而改变了布局，与此同时还能判定出这个棋局是否达到了目标。如果尚未达到目标状态，则以这个新布局作为当前状态，重复上述过程一直进行下去，直至到达目标状态为止。可以看出，用产生式系统来描述和求解这个问题，也是在这个问题空间中去搜索一条从初始状态到达某一个目标状态的路径。这完全可以模拟人们的求解过程，也就是可以把产生式系统作为求解问题思考过程的一种模拟。